
已知函數f(x)= ,試利用基本初等函數的圖象,判斷f(x)有幾個零點,并利用零點存在性定理確定各零點所在的區間(各區間長度不超過1).
,試利用基本初等函數的圖象,判斷f(x)有幾個零點,并利用零點存在性定理確定各零點所在的區間(各區間長度不超過1).
見解析
解析試題分析:本題是一個比較復雜的函數求零點的問題,通過轉化為兩個較熟悉的函數研究.容易得到兩個數有三個交點,所以有三個零點.零點的范圍不好確定,本題很巧妙地應用了零點定理,求出了個的范圍.這種方法值得好好體會.
試題解析:由f(x)=0,得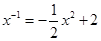 ,令
,令 ,
,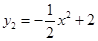 .分別畫出它們的圖象如圖,其中拋物線的頂點坐標為(0,2),與x軸的交點為(-2,0)、(2,0),
.分別畫出它們的圖象如圖,其中拋物線的頂點坐標為(0,2),與x軸的交點為(-2,0)、(2,0),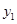 與
與 的圖象有3個交點,從而函數f(x)有3個零點.由f(x)的解析式知x≠0,f(x)的圖象在(-∞,0)和(0,+∞)上分別是連續不斷地曲線,且
的圖象有3個交點,從而函數f(x)有3個零點.由f(x)的解析式知x≠0,f(x)的圖象在(-∞,0)和(0,+∞)上分別是連續不斷地曲線,且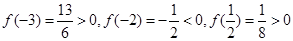
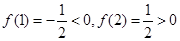 即
即 ,
,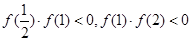 .所以三個零點分別在區間(-3,-2),
.所以三個零點分別在區間(-3,-2),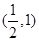 ,(1,2)內.
,(1,2)內.
考點:1.函數的零點轉化為圖解.2.零點定理.3.列舉發現問題的思維.


科目:高中數學 來源: 題型:解答題
如圖是某重點中學學校運動場平面圖,運動場總面積15000平方米,運動場是由一個矩形 和分別以
和分別以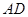 、
、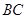 為直徑的兩個半圓組成,塑膠跑道寬8米,已知塑膠跑道每平方米造價為150元,其它部分造價每平方米80元,
為直徑的兩個半圓組成,塑膠跑道寬8米,已知塑膠跑道每平方米造價為150元,其它部分造價每平方米80元,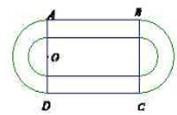
(Ⅰ)設半圓的半徑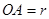 (米),寫出塑膠跑道面積
(米),寫出塑膠跑道面積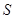 與
與 的函數關系式
的函數關系式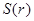 ;
;
(Ⅱ)由于受運動場兩側看臺限制, 的范圍為
的范圍為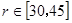 ,問當
,問當 為何值時,運動場造價最低(第2問
為何值時,運動場造價最低(第2問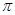 取3近似計算).
取3近似計算).
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知二次函數 ,且不等式
,且不等式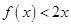 的解集為
的解集為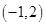 .
.
(1)方程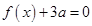 有兩個相等的實根,求
有兩個相等的實根,求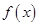 的解析式;
的解析式;
(2)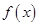 的最小值不大于
的最小值不大于 ,求實數
,求實數 的取值范圍;
的取值范圍;
(3) 如何取值時,函數
如何取值時,函數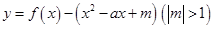 存在零點,并求出零點.
存在零點,并求出零點.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com