
設函數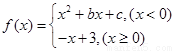 ,若
,若

(1)求函數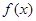 的解析式;
的解析式;
(2)畫出函數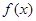 的圖象,并說出函數
的圖象,并說出函數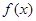 的單調區間;
的單調區間;
(3)若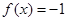 ,求相應
,求相應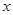 的值.
的值.
(1)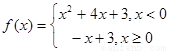 ;(2)增區間為
;(2)增區間為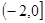 ,減區間為
,減區間為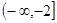 、
、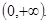 ;
;
(3)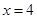 或x=-2。
或x=-2。
【解析】
試題分析:解本小題關鍵是根據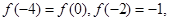 建立b,c的方程,從而解出b,c的值,確定f(x)的解析式,對于分段函數要注意分段求其單調區間.分段畫出其圖像.
建立b,c的方程,從而解出b,c的值,確定f(x)的解析式,對于分段函數要注意分段求其單調區間.分段畫出其圖像.
(1)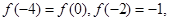
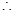
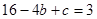 ,
,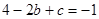 解得
解得
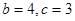
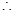
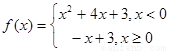 ------------------------------4
------------------------------4
(2)圖象略,--------------------------------------------------6
由圖象可知單調區間為:
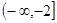 ,
,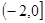 ,
,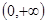 ,其中增區間為
,其中增區間為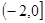 ,
,
減區間為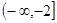 、
、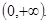 --------------------------------------8
--------------------------------------8
(3)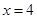 或x=-2----------------------------------------------------------------------12考點:本小題考查了函數的圖像及單調性以及解方程等知識.
或x=-2----------------------------------------------------------------------12考點:本小題考查了函數的圖像及單調性以及解方程等知識.
點評:分段函數在求解單調區間及最值時,要注意分段求解.


 同步練習強化拓展系列答案
同步練習強化拓展系列答案科目:高中數學 來源:2013-2014學年福建省高三12月月考文科數學試卷(解析版) 題型:解答題
設函數 .
.
(1)當 時,求曲線
時,求曲線 在
在 處的切線方程;
處的切線方程;
(2)當 時,求函數
時,求函數 的單調區間;
的單調區間;
(3)在(2)的條件下,設函數 ,若對于
,若對于 [1,2],
[1,2], [0,1],使
[0,1],使 成立,求實數
成立,求實數 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源:2013-2014學年湖南汝城第一中學、長沙實驗中學高三11月聯考文數學卷(解析版) 題型:解答題
設函數 .
.
(1)當 時,求曲線
時,求曲線 在
在 處的切線方程;
處的切線方程;
(2)當 時,求函數
時,求函數 的單調區間;
的單調區間;
(3)在(2)的條件下,設函數 ,若對于
,若對于 [1,2],
[1,2],
 [0,1],使
[0,1],使 成立,求實數
成立,求實數 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源:2014屆廣東省廣州市海珠區高三入學摸底考試文科數學試卷(解析版) 題型:解答題
設函數 .
.
(1)當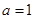 時,求曲線
時,求曲線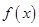 在
在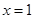 處的切線方程;
處的切線方程;
(2)當 時,求函數
時,求函數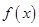 的單調區間;
的單調區間;
(3)在(2)的條件下,設函數 ,若對于
,若對于 [1,2],
[1,2],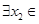 [0,1],使
[0,1],使 成立,求實數
成立,求實數 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com