Question

若正三棱錐底面邊長為1，側棱與底面所成的角為，則其體積為　　．

Answer 1

考點：

棱柱、棱錐、棱臺的體積．

專題：

計算題；空間位置關系與距離．

分析：

欲求正三棱錐的體積，先求正三棱錐的高，由題意，頂點在底面中的射影是底面的中心，從而利用側棱與底面所成角為45°角，可求高，從而得解

解答：

解：先求正三棱錐的高，由題意，頂點P在底面中的射影是底面的中心O，

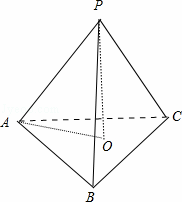
∠PAO為側棱與底面所成角，∠PAO=45°，

從而有高PO=OA==

又底面積S△ABC=×1=

∴正三棱錐的體積V==

故答案為：

點評：

本題主要考查棱錐，線面關系、直線與平面所成的角、點到面的距離等基本知識，同時考查空間想象能力和推理、運算能力．在立體幾何中，求點到平面的距離是一個常見的題型，同時求直線到平面的距離、平行平面間的距離及多面體的體積也常轉化為求點到平面的距離．