
在直角坐標系 中,已知點
中,已知點 ,
, ,
, ,點
,點 在
在 三邊圍成的區域(含邊界)上,且
三邊圍成的區域(含邊界)上,且 .
.
(Ⅰ)若 ,求
,求 ;
;
(Ⅱ)用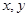 表示
表示 ,并求
,并求 的最小值.
的最小值.
(1)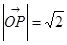 ,(2)
,(2) 的最小值-1.
的最小值-1.
解析試題分析:(1)向量的坐標運算主要是利用加、減、數乘運算法則進行的.若已知有向線段兩端點的的坐標,則應先求出向量的坐標,解題過程中要注意方程的思想的運用及運算法則的正確使用;(2)利用線性規劃求目標函數的最值一般步驟:一畫、二移、三求,其關鍵是準確的作出可行域,理解目標函數的意義;(3)在線性約束條件下,線性目標函數只有在可行域的頂點或者邊界上取得最值.在解答選擇題和填空題時可以根據可行域的頂點直接進行檢驗.
試題解析:解(Ⅰ)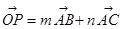
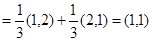 ,
,
∴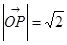 ....................5分
....................5分
由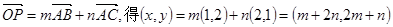 ,
,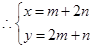 ,
,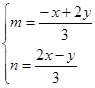 ,
,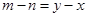
 8分
8分
設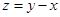 ,直線
,直線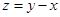 過點
過點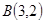 時,
時,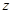 取得最小值-1,即
取得最小值-1,即 的最小值-1
的最小值-1
考點:(1)向量的坐標表示;(2)線性目標函數的最值.


 全優考典單元檢測卷及歸類總復習系列答案
全優考典單元檢測卷及歸類總復習系列答案科目:高中數學 來源: 題型:解答題
某公司計劃2011年在甲、乙兩個電視臺做總時間不超過300分鐘的廣告,廣告費用不超過9萬元.甲、乙電視臺的廣告收費標準分別為500元/分鐘和200元/分鐘.假定甲、乙兩個電視臺為該公司每分鐘所做的廣告,能給公司帶來的收益分別為0.3 萬元和0.2萬元.問:該公司如何分配在甲、乙兩個電視臺的廣告時間,才能使公司收益最大,最大收益是多少萬元?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某企業生產A,B兩種產品,生產每噸產品所需的勞動力和煤、電耗如下表:
已知生產每噸A產品的利潤是5萬元,生產每噸B產品的利潤是10萬元,現因條件限制,該企業僅有勞動力300個,煤360 t,并且供電局只能供電200 kW,試問該企業生產A,B兩種產品各多少噸,才能獲得最大利潤?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某廠生產甲、乙兩種產品每噸所需的煤、電和產值如下表所示.
但國家每天分配給該廠的煤、電有限, 每天供煤至多56噸,供電至多450千瓦,問該廠如何安排生產,使得該廠日產值最大?最大日產值為多少?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
設x,y滿足約束條件 ,
,
(1)畫出不等式表示的平面區域,并求該平面區域的面積;
(2)若目標函數z=ax+by(a>0,b>0)的最大值為4,求 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:單選題
設a,b,c是正數,P=a+b-c,Q=b+c-a,R=c+a-b,則“P·Q·R>0”是“P,Q,R同時大于零”的 ( )
| A.充分不必要條件 | B.必要不充分條件 |
| C.充要條件 | D.既不充分也不必要條件 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com