
設向量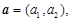
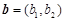 ,定義一種向量積
,定義一種向量積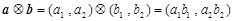 .
.
已知向量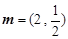 ,
,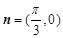 ,點
,點 為
為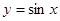 的圖象上的動點,點
的圖象上的動點,點
為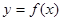 的圖象上的動點,且滿足
的圖象上的動點,且滿足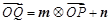 (其中
(其中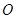 為坐標原點).
為坐標原點).
(1)請用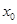 表示
表示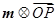 ;
;
(2)求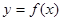 的表達式并求它的周期;
的表達式并求它的周期;
(3)把函數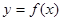 圖象上各點的橫坐標縮小為原來的
圖象上各點的橫坐標縮小為原來的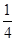 倍(縱坐標不變),得到函數
倍(縱坐標不變),得到函數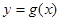 的圖象.設函數
的圖象.設函數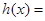
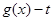
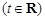 ,試討論函數
,試討論函數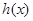 在區間
在區間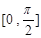 內的零點個數.
內的零點個數.
(1) ;(2)參考解析;(3)參考解析
;(2)參考解析;(3)參考解析
解析試題分析:(1)由向量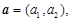
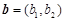 ,定義一種向量積
,定義一種向量積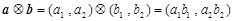 ,所以
,所以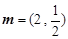 ,
, ,所以根據新定義運算關系可得到
,所以根據新定義運算關系可得到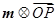 的結果. 點
的結果. 點 為
為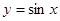 的圖象上的動點,所以可以將
的圖象上的動點,所以可以將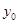 用
用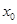 表示即可得結論.
表示即可得結論.
(2)由(1)以及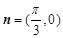 又
又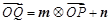 可得
可得 .又點
.又點 為
為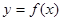 的圖象上的動點,所以可求得函數
的圖象上的動點,所以可求得函數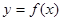 的表達式并求它的周期.
的表達式并求它的周期.
(3)由(2)以及把函數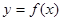 圖象上各點的橫坐標縮小為原來的
圖象上各點的橫坐標縮小為原來的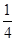 倍,即可得到函數
倍,即可得到函數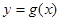 的解析式,以及函數
的解析式,以及函數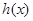 在
在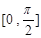 遞增,分類討論即可得到結論.
遞增,分類討論即可得到結論.
(1) , 2分
, 2分
(2) ,
,
所以 , 4分
, 4分
因此 即
即 6分
6分
所以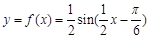 ,它的周期為
,它的周期為 . 8分
. 8分
(3)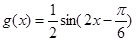 在
在 上單調遞增,在
上單調遞增,在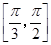 上單調遞減,
上單調遞減,
又 , 10分
, 10分 函數
函數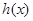 在區間
在區間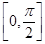 內只有一個零點;
內只有一個零點;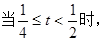 函數
函數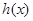 在區間
在區間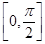 內有兩個零點;
內有兩個零點;
當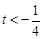 或
或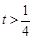 時,函數
時,函數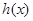 在區間
在區間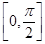 內沒有零點. 12分
內沒有零點. 12分
考點:1.三角函數的性質.2.向量的數量積.3.新定義問題.


 寒假樂園北京教育出版社系列答案
寒假樂園北京教育出版社系列答案科目:高中數學 來源: 題型:解答題
如圖所示,某建筑工地準備建造一間兩面靠墻的三角形露天倉庫堆放材料,已知已有兩面墻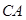 、
、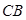 的夾角為
的夾角為 (即
(即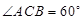 ),現有可供建造第三面圍墻的材料
),現有可供建造第三面圍墻的材料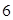 米(兩面墻的長均大于
米(兩面墻的長均大于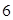 米),為了使得倉庫的面積盡可能大,記
米),為了使得倉庫的面積盡可能大,記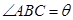 ,問當
,問當 為多少時,所建造的三角形露天倉庫的面積最大,并求出最大值?
為多少時,所建造的三角形露天倉庫的面積最大,并求出最大值? 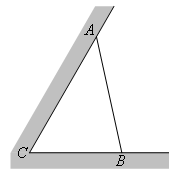
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
電流強度I與時間t的關系式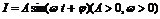 。(1)在一個周期內
。(1)在一個周期內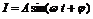 如圖所示,試根據圖象寫出
如圖所示,試根據圖象寫出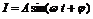 的解析式;(2)為了使
的解析式;(2)為了使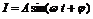 中t在任意一段
中t在任意一段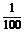 秒的時內I能同時取最大值|A|和最小值-|A|,那么正整數
秒的時內I能同時取最大值|A|和最小值-|A|,那么正整數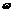 的最小值為多少?
的最小值為多少?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知向量m=(sin x,1),n= ,函數f(x)=(m+n)·m.
,函數f(x)=(m+n)·m.
(1)求函數f(x)的最小正周期T及單調遞增區間;
(2)已知a,b,c分別為△ABC內角A,B,C的對邊,A為銳角,a=2 ,c=4,且f(A)是函數f(x)在
,c=4,且f(A)是函數f(x)在 上的最大值,求△ABC的面積S.
上的最大值,求△ABC的面積S.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知函數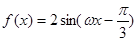 (
(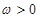 )的最小正周期為
)的最小正周期為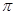 .
.
(1)求函數 的單調增區間;
的單調增區間;
(2)將函數 的圖像向左平移
的圖像向左平移 個單位,再向上平移
個單位,再向上平移 個單位,得到函數
個單位,得到函數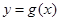 的圖像.求
的圖像.求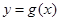 在區間
在區間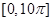 上零點的個數.
上零點的個數.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com