
��֪��(j��ng)�^(gu��)�c(di��n)A����4��0���Ą�(d��ng)ֱ��l�c���タG��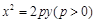 �ཻ��B��C����(d��ng)ֱ��l��б����
�ཻ��B��C����(d��ng)ֱ��l��б����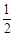 �r(sh��)��
�r(sh��)��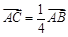 ��
��
�������タG�ķ��̣�
�����O(sh��)����BC�Ĵ�ֱƽ�־���y�S�ϵĽؾ���b����b��ȡֵ������
����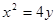 ������
������
����ԇ�}������ԓ�}���쒁�タ�ķ��̡��f�_(d��)������ֱ���͒��タ��λ���P(gu��n)ϵ�������Ȼ��A(ch��)֪�R(sh��)�����씵(sh��)�νY(ji��)�ϡ��C�Ϸ����ͽ�Q��(w��n)�}�����������\(y��n)��������������ֱ��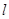 �ķ��̣�
�ķ��̣�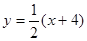 ���͒��タ
���͒��タ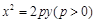 (li��n)������
(li��n)������
�O(sh��)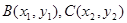 ������ ����ʽ
������ ����ʽ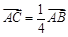 �У���
�У���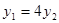 ��Ȼ��(li��n)��
��Ȼ��(li��n)��
�ɵ� ��
��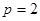 �������タ���̞�
�������タ���̞�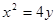 �������O(sh��)ֱ��
�������O(sh��)ֱ��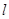 �ķ��̣�
�ķ��̣�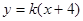 ��
��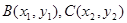 ������
������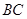 �����c(di��n)
�����c(di��n)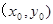 ����
����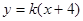 �c
�c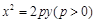 (li��n)�����ɵ�
(li��n)�����ɵ�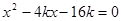 ����?y��n)�ֱ���c���タ���c���c(di��n)
����?y��n)�ֱ���c���タ���c���c(di��n)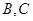 ������
������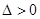 ���ɵ�
���ɵ�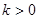 ��
��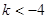 ���ٱ�ʾ���c(di��n)
���ٱ�ʾ���c(di��n)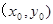 ���M(j��n)������
���M(j��n)������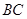 ���д������̣���
���д������̣���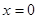 ���ɵ�����
���ɵ����� �S�Ľؾ�
�S�Ľؾ�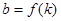 ������ֵ��.
������ֵ��.
ԇ�}������(1)�O(sh��)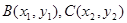 ������֪k1��
������֪k1��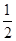 �r(sh��)��l���̞�
�r(sh��)��l���̞�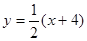
��x��2y��4��
�� ��
��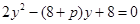
��
�֡�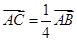
�� 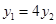 5��
5��
��p��0��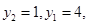 ��
��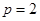 �������タ���̞飺
�������タ���̞飺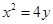 ��
��
(2)�O(sh��)l�� ��BC���c(di��n)����(bi��o)��
��BC���c(di��n)����(bi��o)��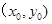
��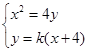 �ã�
�ã�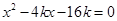 ��
��
��x0��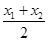 ��2k��y0��k(x0��4)��2k2��4k��
��2k��y0��k(x0��4)��2k2��4k��
��BC���д������̞�y?2k2?4k��?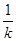 (x?2k)
(x?2k)
��BC���д�����y�S�ϵĽؾ��飺b��2k2��4k��2��2(k��1)2
��(du��)�ڷ��̢��ɡ���16k2��64k��0�ã�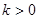 ��
��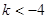 ��
��
��  12��
12��
���c(di��n)��1�����タ�Ę�(bi��o)��(zh��n)���̣�2���f�_(d��)������3��ֱ������.



| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��֪?ji��ng)ӈA��(j��ng)�^(gu��)�c(di��n) ���Һ�ֱ��
���Һ�ֱ��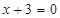 ���У�
����
��1�����(d��ng)�A�A�ĵ�܉�EC�ķ��̣�
��2����֪����C��һ�c(di��n)M����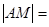 5����M�c(di��n)������(bi��o)��
5����M�c(di��n)������(bi��o)��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��֪�E�A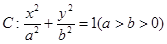 �����ҽ��c(di��n)�քe��
�����ҽ��c(di��n)�քe��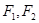 ���x����
���x����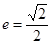 ��
��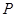 ��E�A����һ�c(di��n)����
��E�A����һ�c(di��n)����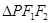 �������e��
�������e��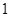 .
.
������E�A �ķ��̣�
�ķ��̣�
�����O(sh��)б�ʞ� ��ֱ��
��ֱ��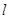 ���E�A
���E�A ��
��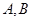 ���c(di��n)������
���c(di��n)������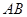 ��ֱ���ĈA���^(gu��)ԭ�c(di��n)
��ֱ���ĈA���^(gu��)ԭ�c(di��n) ����(sh��)��(sh��)
����(sh��)��(sh��) �M��l��
�M��l��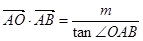 ����
���� �����ֵ.
�����ֵ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��֪�E�A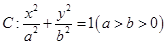 �^(gu��)�c(di��n)
�^(gu��)�c(di��n)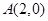 ,�x���ʞ�
,�x���ʞ�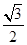 .
.
������E�A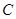 �ķ��̣�
�ķ��̣�
�����^(gu��)�c(di��n)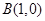 ��б�ʞ�
��б�ʞ� ��
��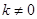 ����ֱ��
����ֱ��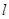 �c�E�A
�c�E�A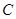 �ཻ��
�ཻ��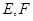 ���c(di��n)��ֱ��
���c(di��n)��ֱ�� ��
��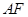 �քe��ֱ��
�քe��ֱ��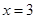 ��
��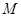 ��
��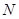 ���c(di��n),����
���c(di��n),���� �����c(di��n)��
�����c(di��n)�� .ӛֱ��
.ӛֱ��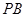 ��б�ʞ�
��б�ʞ�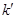 �����C:
�����C: 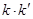 �鶨ֵ.
�鶨ֵ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
�O(sh��)���タ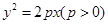 �Ľ��c(di��n)��
�Ľ��c(di��n)��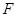 �����(zh��n)���c
�����(zh��n)���c �S�Ľ��c(di��n)��
�S�Ľ��c(di��n)�� ���^(gu��)
���^(gu��) �c(di��n)��ֱ��
�c(di��n)��ֱ��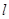 �����タ��
�����タ��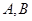 ���c(di��n)��
���c(di��n)��
��1����ֱ��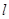 ��б�ʞ�
��б�ʞ�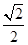 �����C��
�����C��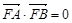 ��
��
��2���O(sh��)ֱ��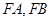 ��б�ʷքe��
��б�ʷքe��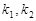 ����
����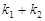 ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��֪��ABC��, �c(di��n)A��B������(bi��o)�քe��A���� ��0����B��
��0����B�� ��0���c(di��n)C��x�S�Ϸ���
��0���c(di��n)C��x�S�Ϸ���
�������c(di��n)C����(bi��o)�飨 ��1��������A��B�齹�c(di��n)�ҽ�(j��ng)�^(gu��)�c(di��n)C�ęE�A�ķ��̣�
��1��������A��B�齹�c(di��n)�ҽ�(j��ng)�^(gu��)�c(di��n)C�ęE�A�ķ��̣�
�����^(gu��)�c(di��n)P��m��0�����Aб�Ǟ� ��ֱ��l����1����������M��N���c(di��n)�����c(di��n)Q��1��0��ǡ���Ծ���MN��ֱ���ĈA�ϣ���(sh��)��(sh��)m��ֵ��
��ֱ��l����1����������M��N���c(di��n)�����c(di��n)Q��1��0��ǡ���Ծ���MN��ֱ���ĈA�ϣ���(sh��)��(sh��)m��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��D����֪���タ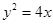 �Ľ��c(di��n)��F
�Ľ��c(di��n)��F �^(gu��)�c(di��n)
�^(gu��)�c(di��n)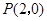 ��ֱ�������タ��A
��ֱ�������タ��A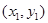 ��B
��B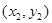 ���c(di��n)��ֱ��AF��BF�քe�c���タ�����c(di��n)M��N
���c(di��n)��ֱ��AF��BF�քe�c���タ�����c(di��n)M��N 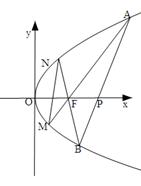
��1����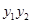 ��ֵ��
��ֵ��
��2��ӛֱ��MN��б�ʞ�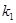 ��ֱ��AB��б�ʞ�
��ֱ��AB��б�ʞ�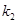 �C����
�C����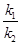 �鶨ֵ
�鶨ֵ
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��֪�E�A��������ԭ�c(di��n)�����c(di��n)��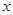 �S�ϣ�������
�S�ϣ�������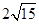 ���ҽ�(j��ng)�^(gu��)�c(di��n)
���ҽ�(j��ng)�^(gu��)�c(di��n) ��ֱ��
��ֱ��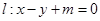 ���E�A�ڲ�ͬ�ă��c(di��n)A��B.
���E�A�ڲ�ͬ�ă��c(di��n)A��B.
(1)�� ��ȡֵ��������
��ȡֵ��������
(2)��ֱ��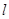 ����(j��ng)�^(gu��)�c(di��n)
����(j��ng)�^(gu��)�c(di��n)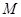 �����C��ֱ��
�����C��ֱ��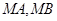 ��б�ʻ����෴��(sh��).
��б�ʻ����෴��(sh��).
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��֪�E�A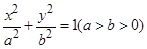 ���L(zh��ng)�S�ɶ��c(di��n)�քe��
���L(zh��ng)�S�ɶ��c(di��n)�քe�� ��
��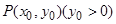 �ǙE�A�ϵĄ�(d��ng)�c(di��n)����
�ǙE�A�ϵĄ�(d��ng)�c(di��n)���� ��һ߅��
��һ߅�� �S�·�������
�S�·������� ��ʹ
��ʹ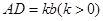 ��
��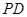 ��
�� ���c(di��n)
���c(di��n)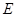 ��
��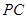 ��
�� ���c(di��n)
���c(di��n)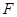 ��
��
������D��1������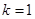 ����
���� ��E�A����c(di��n)�r(sh��)��
��E�A����c(di��n)�r(sh��)��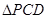 ����e��12���c(di��n)
����e��12���c(di��n)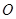 ��ֱ��
��ֱ��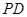 �ľ��x��
�ľ��x��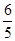 ����E�A�ķ��̣�
����E�A�ķ��̣�
������D��2������ ��ԇ�C����
��ԇ�C����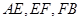 �ɵȱȔ�(sh��)�У�
�ɵȱȔ�(sh��)�У�
�鿴�𰸺ͽ���>>
��(gu��)�H�W(xu��)У��(y��u)�x - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)��(zhu��n)�^(q��) | ����p�_�e��(b��o)��(zhu��n)�^(q��) | ��vʷ̓�o(w��)���x�к���Ϣ�e��(b��o)��(zhu��n)�^(q��) | �����֙�(qu��n)�e��(b��o)��(zhu��n)�^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com