
已知△ABC中, 點A,B的坐標分別為A(- ,0),B(
,0),B( ,0)點C在x軸上方.
,0)點C在x軸上方.
(Ⅰ)若點C坐標為( ,1),求以A,B為焦點且經(jīng)過點C的橢圓的方程:
,1),求以A,B為焦點且經(jīng)過點C的橢圓的方程:
(Ⅱ)過點P(m,0)作傾斜角為 的直線l交(1)中曲線于M,N兩點,若點Q(1,0)恰在以線段MN為直徑的圓上,求實數(shù)m的值.
的直線l交(1)中曲線于M,N兩點,若點Q(1,0)恰在以線段MN為直徑的圓上,求實數(shù)m的值.
(Ⅰ)橢圓方程為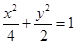 ;(Ⅱ)
;(Ⅱ)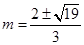 .
.
解析試題分析:(Ⅰ)由橢圓定義易求;(Ⅱ)此題是直線與橢圓位置關系的問題,可采用設而不求的解題方法,設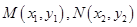 ,由已知可得直線
,由已知可得直線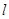 的方程為
的方程為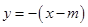 ,代入橢圓方程,得到關于
,代入橢圓方程,得到關于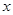 的一元二次方程,注意到點P(m,0)不一定在橢圓內部,需對方程是否有解討論, 點
的一元二次方程,注意到點P(m,0)不一定在橢圓內部,需對方程是否有解討論, 點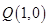 恰在以線段
恰在以線段 為直徑的圓上,說明
為直徑的圓上,說明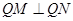 ,它們的斜率互為負倒數(shù),利用根與系數(shù)關系,建立方程,從而求出實數(shù)m的值.此題易錯點,不知對方程是否有解討論.
,它們的斜率互為負倒數(shù),利用根與系數(shù)關系,建立方程,從而求出實數(shù)m的值.此題易錯點,不知對方程是否有解討論.
試題解析:(Ⅰ)設橢圓方程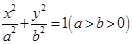 ,
,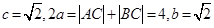 ,
,
橢圓方程為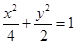 ;
;
(Ⅱ)直線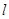 的方程為
的方程為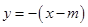 ,令
,令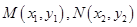 ,聯(lián)立方程得:
,聯(lián)立方程得: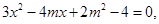
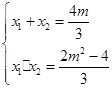 ,
,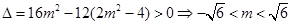 ,
,
若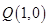 恰在以線段
恰在以線段 為直徑的圓上,則
為直徑的圓上,則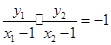 ,即
,即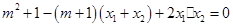 ,
, 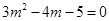 ,解得
,解得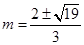 ,
,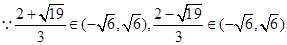 ,
,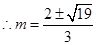 符合題意
符合題意
考點:橢圓的方程,直線與橢圓的位置關系,考查學生的運算能力、化簡能力以及數(shù)形結合的能力.


科目:高中數(shù)學 來源: 題型:解答題
如圖,F(xiàn)1,F(xiàn)2分別是橢圓C: +
+ =1(a>b>0)的左、右焦點,A是橢圓C的頂點,B是直線AF2與橢圓C的另一個交點,∠F1AF2=60°
=1(a>b>0)的左、右焦點,A是橢圓C的頂點,B是直線AF2與橢圓C的另一個交點,∠F1AF2=60°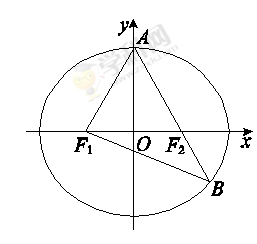
(1)求橢圓C的離心率;
(2)已知△AF1B的面積為40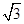 ,求a,b的值
,求a,b的值
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
已知拋物線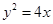 的焦點為F2,點F1與F2關于坐標原點對稱,以F1,F2為焦點的橢圓C過點
的焦點為F2,點F1與F2關于坐標原點對稱,以F1,F2為焦點的橢圓C過點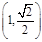 .
.
(Ⅰ)求橢圓C的標準方程;
(Ⅱ)設點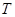
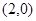 ,過點F2作直線
,過點F2作直線 與橢圓C交于A,B兩點,且
與橢圓C交于A,B兩點,且 ,若
,若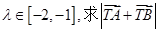 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
知橢圓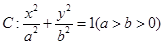 的離心率為
的離心率為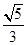 ,定點
,定點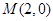 ,橢圓短軸的端點是
,橢圓短軸的端點是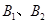 ,且
,且 .
.
(1)求橢圓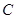 的方程;
的方程;
(2)設過點 且斜率不為0的直線交橢圓
且斜率不為0的直線交橢圓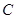 于
于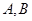 兩點.試問
兩點.試問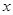 軸上是否存在異于
軸上是否存在異于 的定點
的定點 ,使
,使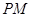 平分
平分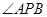 ?若存在,求出點
?若存在,求出點 的坐標;若不存在,說明理由.
的坐標;若不存在,說明理由.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
已知經(jīng)過點A(-4,0)的動直線l與拋物線G: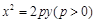 相交于B、C,當直線l的斜率是
相交于B、C,當直線l的斜率是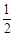 時,
時,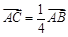 .
.
(Ⅰ)求拋物線G的方程;
(Ⅱ)設線段BC的垂直平分線在y軸上的截距為b,求b的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
某跳水運動員在一次跳水訓練時的跳水曲線為如圖所示的拋物線一段,已知跳水板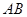 長為2m,跳水板距水面
長為2m,跳水板距水面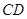 的高
的高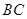 為3m,
為3m, =5m,
=5m,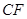 =6m,為安全和空中姿態(tài)優(yōu)美,訓練時跳水曲線應在離起跳點
=6m,為安全和空中姿態(tài)優(yōu)美,訓練時跳水曲線應在離起跳點 m(
m(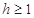 )時達到距水面最大高度4m,規(guī)定:以
)時達到距水面最大高度4m,規(guī)定:以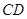 為橫軸,
為橫軸,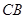 為縱軸建立直角坐標系.
為縱軸建立直角坐標系.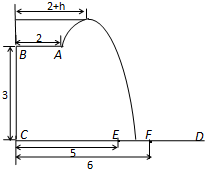
(1)當 =1時,求跳水曲線所在的拋物線方程;
=1時,求跳水曲線所在的拋物線方程;
(2)若跳水運動員在區(qū)域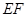 內入水時才能達到壓水花的訓練要求,求達到壓水花的訓練要求時
內入水時才能達到壓水花的訓練要求,求達到壓水花的訓練要求時 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
如圖,橢圓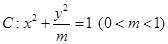 的左頂點為
的左頂點為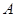 ,
,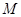 是橢圓
是橢圓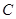 上異于點
上異于點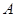 的任意一點,點
的任意一點,點 與點
與點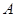 關于點
關于點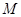 對稱.
對稱.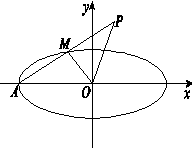
(1)若點 的坐標為
的坐標為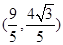 ,求
,求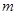 的值;
的值;
(2)若橢圓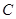 上存在點
上存在點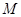 ,使得
,使得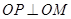 ,求
,求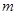 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
設橢圓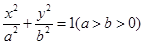 的左焦點為
的左焦點為 ,離心率為
,離心率為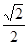 ,過點
,過點 且與
且與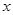 軸垂直的直線被橢圓截得的線段長為
軸垂直的直線被橢圓截得的線段長為 .
.
(1) 求橢圓方程.
(2) 過點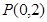 的直線
的直線 與橢圓交于不同的兩點
與橢圓交于不同的兩點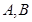 ,當
,當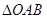 面積最大時,求
面積最大時,求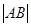 .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
已知橢圓C: 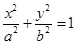 (a>b>0)的兩個焦點和短軸的兩個端點都在圓
(a>b>0)的兩個焦點和短軸的兩個端點都在圓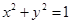 上.
上.
(I)求橢圓C的方程;
(II)若斜率為k的直線過點M(2,0),且與橢圓C相交于A, B兩點.試探討k為何值時,三角形OAB為直角三角形.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com