
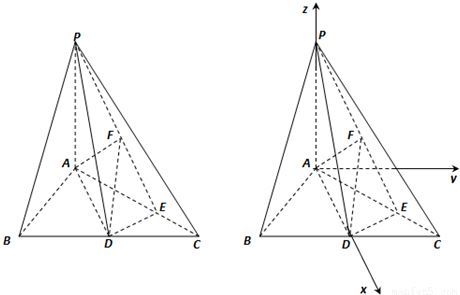
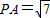 ,點D是BC的中點,點E在AC上,且DE⊥AC.
,點D是BC的中點,點E在AC上,且DE⊥AC.
 解:(1)∵PA⊥底面ABC,DE?底面ABC,
解:(1)∵PA⊥底面ABC,DE?底面ABC,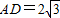 ,
,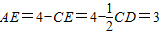 .
.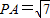 ,所以
,所以 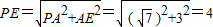 ,
,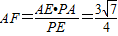 ,
,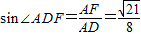 .-------(13分)
.-------(13分)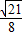 .-------------(14分)
.-------------(14分)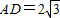 ,AE=3,
,AE=3,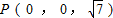 ,
,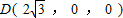 ,
,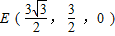 .-----(6分)
.-----(6分)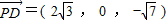 ,
,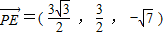 ,
,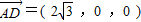 .---(8分)
.---(8分)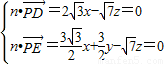
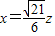 ,
,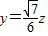 .
.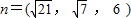 .-------(11分)
.-------(11分)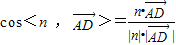 =
=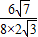 =
=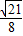 .------(13分)
.------(13分)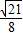 .-----------(14分)
.-----------(14分)

 全優沖刺100分系列答案
全優沖刺100分系列答案 英才點津系列答案
英才點津系列答案科目:高中數學 來源: 題型:
 如圖,三角ABC是邊長為4正三角形,PA⊥底面ABC,PA=
如圖,三角ABC是邊長為4正三角形,PA⊥底面ABC,PA=| 7 |
查看答案和解析>>
科目:高中數學 來源:2012-2013學年湖北荊州、黃岡、襄陽、十堰、宜昌、孝感、恩施七市高三4月聯考文數學卷(解析版) 題型:填空題
某三棱錐P-ABC的正視圖為如圖所示邊長為2的正三角形,俯視圖為等腰直角三角 形,則三棱錐的表面積是______.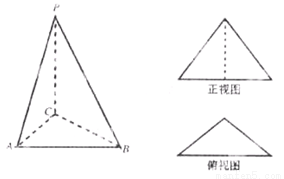
查看答案和解析>>
科目:高中數學 來源:2011-2012學年廣東省佛山市高二(上)期末數學試卷(理科)(解析版) 題型:解答題
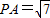 ,點D是BC的中點,點E在AC上,且DE⊥AC.
,點D是BC的中點,點E在AC上,且DE⊥AC.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com