
思路解析:此類問題應由f(1)、f(2)整體代入,否則單獨求9a或c的范圍,易導致范圍擴大.
解法一:∵f(x)=ax2+c,∴![]()
解得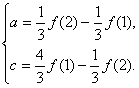 ∴f(3)=9a+c=
∴f(3)=9a+c=![]() f(2)-
f(2)-![]() f(1).
f(1).
∵-2≤f(2)≤3,∴-![]() ≤
≤![]() f(2)≤8.①
f(2)≤8.①
又∵-3≤f(1)≤1,∴-![]() ≤-
≤-![]() f(1)≤5.②
f(1)≤5.②
①+②,得-![]() -
-![]() ≤
≤![]() f(2)-
f(2)-![]() f(1)≤8+5,即-7≤f(3)≤13.
f(1)≤8+5,即-7≤f(3)≤13.
∴f(3)的最大值是13,最小值是-7.
解法二:由已知f(1)=a+c,f(2)=4a+c,f(3)=9a+c,
設存在實數m,n使9a+c=m(a+c)+n(4a+c),
即9a+c=(m+4n)a+(m+n)c.
∴![]() 解得
解得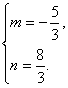
∴-![]() ≤-
≤-![]() (a+c)≤5,-
(a+c)≤5,-![]() ≤
≤![]() (4a+c)≤8.
(4a+c)≤8.
上兩式相加,得-7≤9a+c≤13,即-7≤f(3)≤13.
故f(3)的最大值是13,最小值是-7.


科目:高中數學 來源: 題型:
| ax2+bx |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com