
在數列{an}(n∈N*)中,已知a1=1,a2k=-ak,a2k-1=(-1)k+1ak,k∈N*. 記數列{an}的前n項和為Sn.
(1)求S5,S7的值;
(2)求證:對任意n∈N*,Sn≥0.
(1) S5=3,S7=1.
(2)根據已知的遞推關系,然后結合整體的思想來分析得到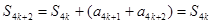 ,然后運用數學歸納法加以證明。
,然后運用數學歸納法加以證明。
解析試題分析:解:(1)根據題意, 由于a1=1,a2k=-ak,a2k-1=(-1)k+1ak,
故有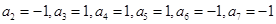 故可知S5=3,S7=1. 2分
故可知S5=3,S7=1. 2分
(2)由題設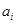 的定義可知,對于每個正整數k,有
的定義可知,對于每個正整數k,有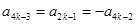 . ①
. ①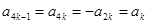 . ② 4分
. ② 4分
則 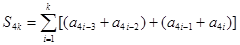
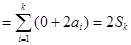 ,③
,③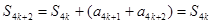 . ④ 6分
. ④ 6分
下面證明對于所有的n≥1,Sn≥0.
對于k,用數學歸納法予以證明.
當i=1,2,3,4,即k=0時,S1=1,S2=0, S3=1, S4=2.
假設對于所有的i≤4k,Si≥0,則由①、②、③、④知,
S4k+4=2Sk+1≥0,
S4k+2=S4k≥0,
S4k+3=S4k+2+a4k+3=S4k+2+a4k+4=S4k+2+(S4k+4-S4k+3),S4k+3=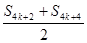 ≥0.
≥0.
接下來證明:S4k+1≥0.
若k是奇數,則S4k=2Sk≥2.
因為k是奇數,所以由題設知數列的各項均為奇數,可知Sk也是一個奇數. 于是
S4k≥2. 因此,S4k+1=S4k+a4k+1≥1.
若k是偶數,則a4k+1=a2k+1=ak+1. 所以S4k+1=S4k+a4k+1=2Sk+ak+1=Sk+Sk+1≥0.
綜上,對于所有的n≥1,Sn≥0. 10分
考點:數列的遞推關系的運用
點評:解題的關鍵是通過具體的例子歸納猜想結論,結合數學歸納法加以證明,屬于中檔題。


科目:高中數學 來源: 題型:解答題
已知函數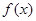
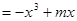 在
在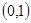 上是增函數
上是增函數
(1)求實數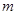 的取值集合
的取值集合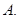
(2)當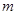 取值集合
取值集合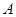 中的最小值時, 定義數列
中的最小值時, 定義數列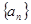 ;滿足
;滿足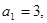 且
且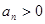 ,
, 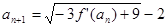 , 設
, 設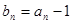 , 證明:數列
, 證明:數列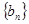 是等比數列, 并求數列
是等比數列, 并求數列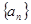 的通項公式.
的通項公式.
(3)若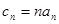 , 數列
, 數列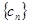 的前
的前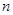 項和為
項和為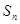 , 求
, 求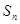 .
.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知 ,數列
,數列 滿足
滿足 ,數列
,數列 滿足
滿足 ;又知數列
;又知數列 中,
中, ,且對任意正整數
,且對任意正整數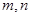 ,
, .
.
(Ⅰ)求數列 和數列
和數列 的通項公式;
的通項公式;
(Ⅱ)將數列 中的第
中的第 項,第
項,第 項,第
項,第 項,……,第
項,……,第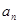 項,……刪去后,剩余的項按從小到大的順序排成新數列
項,……刪去后,剩余的項按從小到大的順序排成新數列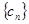 ,求數列
,求數列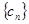 的前
的前 項和.
項和.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
設各項均為正實數的數列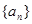 的前
的前 項和為
項和為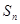 ,且滿足
,且滿足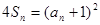 (
(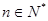 ).
).
(Ⅰ)求數列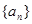 的通項公式;
的通項公式;
(Ⅱ)設數列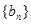 的通項公式為
的通項公式為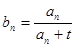 (
(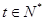 ),若
),若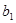 ,
,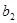 ,
,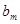 (
(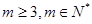 )成等差數列,求
)成等差數列,求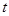 和
和 的值;
的值;
(Ⅲ)證明:存在無窮多個三邊成等比數列且互不相似的三角形,其三邊長為數列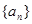 中的三項
中的三項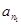 ,
,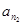 ,
,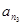 .
.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題滿分13分)
在數列{an}中,a1=1,an=n2[1+ +
+ +…+
+…+ ] (n≥2,n∈N)
] (n≥2,n∈N)
(1)當n≥2時,求證: =
=
(2)求證:(1+ )(1+
)(1+ )…(1+
)…(1+ )<4
)<4
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com