中文字幕人妻色偷偷久久-精品久久久久成人码免费动漫-久久精品国产清自在天天线-国产成人精品免高潮在线观看

精英家教網 > 高中數學 > 題目詳情

已知函數f(x)＝x2－2x，x∈[a，b]的值域為[－1，3]，則b－a的取值范圍是________．

 

[2，4]

【解析】f(x)＝x2－2x＝(x－1)2－1，因為x∈[a，b]的值域為[－1，3]，所以當a＝－1時，1≤b≤3；當b＝3時，－1≤a≤1，所以b－a∈[2，4]．

 

練習冊系列答案
相關習題

科目：高中數學 來源：2013-2014學年高考數學總復習考點引領+技巧點撥第二章第5課時練習卷（解析版） 題型：解答題

已知函數f(x)＝ax3－3ax，g(x)＝bx2＋clnx，且g(x)在點(1，g(1))處的切線方程為2y－1＝0.

(1)求g(x)的解析式；

(2)設函數G(x)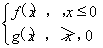＝若方程G(x)＝a2有且僅有四個解，求實數a的取值范圍．

 

查看答案和解析>>

科目：高中數學 來源：2013-2014學年高考數學總復習考點引領+技巧點撥第二章第3課時練習卷（解析版） 題型：填空題

給定函數：①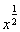y＝，②y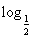＝(x＋1)，③y＝|x－1|，④y＝2x＋1，其中在區間(0，1)上單調遞減的函數是____________．(填序號)

 

查看答案和解析>>

科目：高中數學 來源：2013-2014學年高考數學總復習考點引領+技巧點撥第二章第2課時練習卷（解析版） 題型：填空題

設函數g(x)＝x2－2(x∈R)，f(x)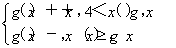＝則f(x)的值域是________．

 

查看答案和解析>>

科目：高中數學 來源：2013-2014學年高考數學總復習考點引領+技巧點撥第二章第2課時練習卷（解析版） 題型：解答題

求下列函數的值域：

(1) f(x)＝；

(2) g(x)＝；

(3) y＝log3x＋logx3－1.

 

查看答案和解析>>

科目：高中數學 來源：2013-2014學年高考數學總復習考點引領+技巧點撥第二章第1課時練習卷（解析版） 題型：填空題

集合M＝{f(x)|存在實數t使得函數f(x)滿足f(t＋1)＝f(t)＋f(1)}，則下列函數(a、b、c、k都是常數)：

① y＝kx＋b(k≠0，b≠0)；② y＝ax2＋bx＋c(a≠0)；

③ y＝ax(0<a<1)；④ y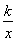＝(k≠0)；⑤ y＝sinx.

其中屬于集合M的函數是________．(填序號)

 

查看答案和解析>>

科目：高中數學 來源：2013-2014學年高考數學總復習考點引領+技巧點撥第二章第1課時練習卷（解析版） 題型：解答題

求下列函數f(x)的解析式．

(1) 已知f(1－x)＝2x2－x＋1，求f(x)；

(2) 已知f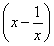＝x2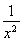＋，求f(x)；

(3) 已知一次函數f(x)滿足f(f(x))＝4x－1，求f(x)；

(4) 定義在(－1，1)內的函數f(x)滿足2f(x)－f(－x)＝lg(x＋1)，求f(x)．

 

查看答案和解析>>

科目：高中數學 來源：2013-2014學年高考數學總復習考點引領+技巧點撥第二章第14課時練習卷（解析版） 題型：解答題

已知f(x)＝xlnx，g(x)＝－x2＋ax－3.

(1)求函數f(x)在[t，t＋2](t>0)上的最小值；

(2)對一切x∈(0，＋∞)，2f(x)≥g(x)恒成立，求實數a的取值范圍；

(3)證明對一切x∈(0，＋∞)，都有lnx>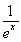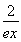－成立．

 

查看答案和解析>>

科目：高中數學 來源：2013-2014學年高考數學總復習考點引領+技巧點撥第二章第12課時練習卷（解析版） 題型：解答題

請你設計一個包裝盒，如圖所示，ABCD是邊長為60cm的正方形硬紙片，切去陰影部分所示的四個全等的等腰直角三角形，再沿虛線折起，使得A、B、C、D四個點重合于圖中的點P，正好形成一個正四棱柱形狀的包裝盒，E、F在AB上是被切去的等腰直角三角形斜邊的兩個端點，設AE＝FB＝xcm.

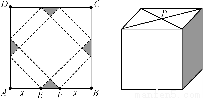
(1)某廣告商要求包裝盒側面積S(cm2)最大，試問x應取何值？

(2)某廠商要求包裝盒容積V(cm3)最大，試問x應取何值？并求出此時包裝盒的高與底面邊長的比值．

 

查看答案和解析>>

同步練習冊答案