
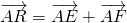 的點R必在圓B上.
的點R必在圓B上.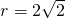 ,
,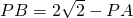 ,
, ,
, .
. ,即m2+2n2=2.
,即m2+2n2=2.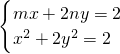 ,
,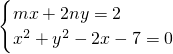
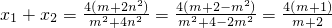 ,
,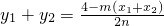 =
=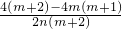 =
=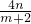 .
.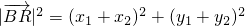
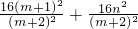
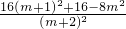
 ,
,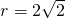 ,知
,知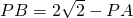 ,由此能求出動圓圓心P的軌跡Ω的方程.
,由此能求出動圓圓心P的軌跡Ω的方程.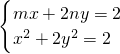 ,得x2-2mx+m2=0,由此能導出直線l與曲線Ω有唯一的公共點.
,得x2-2mx+m2=0,由此能導出直線l與曲線Ω有唯一的公共點. ,故點R在圓B上.
,故點R在圓B上.

 閱讀快車系列答案
閱讀快車系列答案科目:高中數(shù)學 來源: 題型:
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
| AR |
| AE |
| AF |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
| 1 |
| 4a |
| 1 |
| 4a |
| NA |
| NB |
查看答案和解析>>
科目:高中數(shù)學 來源:2010-2011學年陜西省西安市八校高三聯(lián)考數(shù)學試卷4(理科)(解析版) 題型:解答題
 的點R必在圓B上.
的點R必在圓B上.查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com