Question

已知直線l經過點P(1,1)，傾斜角．

（1）寫出直線l的參數方程；

（2）設l與圓相交于兩點A,B，求點P到A,B兩點的距離之積．

 

Answer 1

【答案】

（1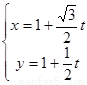）  ；（2）點P到A,B兩點的距離之積為2．

【解析】

試題分析：（1）利用公式和已知條件直線l經過點P（1，1），傾斜角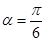，寫出其極坐標再化為一般參數方程；

（2）由題意將直線 代入x²+y²=4，從而求解．

（1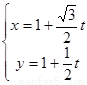）  ；---------------5分

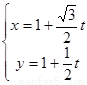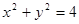（2）把直線 代入，得：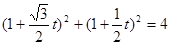

所以 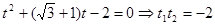，則點P到A,B兩點的距離之積為2．----10分

考點：本題主要考查了參數方程與普通方程的區別和聯系，兩者要會互相轉化，根據實際情況選擇不同的方程進行求解，這也是每年高考必的熱點問題。

點評：解決該試題的關鍵是利用直線方程得到其參數方程，聯立方程組來得到參數t滿足的關系式，進而運用參數的幾何意義得到求解。