
設函數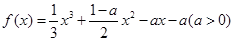 .
.
(1)若函數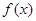 在區間(-2,0)內恰有兩個零點,求a的取值范圍;
在區間(-2,0)內恰有兩個零點,求a的取值范圍;
(2)當a=1時,求函數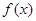 在區間[t,t+3]上的最大值.
在區間[t,t+3]上的最大值.
(1)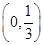 (2)
(2)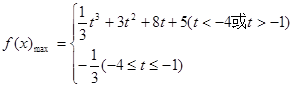
解析試題分析:
科目:高中數學
來源:
題型:解答題
據統計某種汽車的最高車速為120千米∕時,在勻速行駛時每小時的耗油量
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
(1)根據題意對函數 求導,獲得導函數
求導,獲得導函數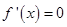 的根與大于0小于0的解集,獲得函數
的根與大于0小于0的解集,獲得函數 的單調區間和極值點,極值.進而確定函數
的單調區間和極值點,極值.進而確定函數 在區間
在區間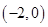 上的單調性,再利用數形結合的思想與零點存在性定理的知識可以得到函數在
上的單調性,再利用數形結合的思想與零點存在性定理的知識可以得到函數在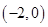 上要有兩個零點,需要
上要有兩個零點,需要 滿足
滿足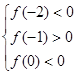 即可,解不等式即可求出
即可,解不等式即可求出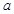 的取值范圍.
的取值范圍.
(2)根據題意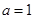 ,則利用(1)可以得到
,則利用(1)可以得到 的單調性以及極值點,極值.要得到函數
的單調性以及極值點,極值.要得到函數 在含參數的區間
在含參數的區間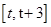 上的最大值,我們需要討論
上的最大值,我們需要討論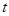 的范圍得到函數
的范圍得到函數 的在區間
的在區間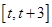 上的單調性進而得到
上的單調性進而得到 在該區間上的最大值,為此分三種情況分別為
在該區間上的最大值,為此分三種情況分別為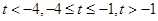 ,依次確定單調性得到最大值即可.
,依次確定單調性得到最大值即可.
試題解析:
(1)∵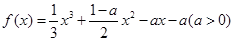
∴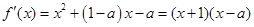 , (1分)
, (1分)
令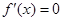 ,解得
,解得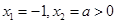 (2分)
(2分)
當x變化時,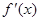 ,
,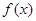 的變化情況如下表:
的變化情況如下表:
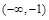
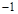


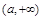
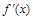
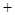
0 — 0 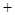
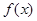
↗ 極大值 ↘ 極小值 

優秀生數法題解系列答案
亮點激活精編全能大試卷系列答案
成長背囊高效測評單元測試卷系列答案
伴你成長同步輔導與能力訓練系列答案
黃岡金牌之路單元月考卷系列答案
伴你成長階段綜合測試卷集系列答案
紅領巾樂園沈陽出版社系列答案
思維體操系列答案
輕松奪冠單元期末沖刺100分系列答案

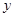 (升)與行駛速度
(升)與行駛速度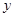 (千米∕時)之間有如下函數關系:
(千米∕時)之間有如下函數關系: 。已知甲、乙兩地相距100千米。
。已知甲、乙兩地相距100千米。
(1)若汽車以40千米∕時的速度勻速行駛,則從甲地到乙地需耗油多少升?
(2)當汽車以多大的速度勻速行駛時,從甲地到乙地耗油最少?最少為多少升?
版權聲明:本站所有文章,圖片來源于網絡,著作權及版權歸原作者所有,轉載無意侵犯版權,如有侵權,請作者速來函告知,我們將盡快處理,聯系qq:3310059649。
ICP備案序號: 滬ICP備07509807號-10 鄂公網安備42018502000812號