
已知函數 .
.
(1)若函數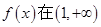 上是減函數,求實數a的最小值;
上是減函數,求實數a的最小值;
(2)若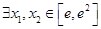 ,使
,使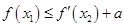 成立,求實數a的取值范圍.
成立,求實數a的取值范圍.
(1)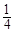 (2)
(2)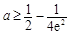 .
.
解析試題分析:(1) 根據原函數在區間上的單調遞減轉化為導數在該區間內小于等于零恒成立,再把恒成立轉化為最值求解,在求解的過程中利用了二次三項式的配方;(2)命題的等價變換是解決本小題的關鍵,“若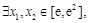 使
使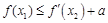 成立”等價于 “當
成立”等價于 “當 時,有
時,有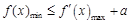 ”,于是整個問題就化為求函數的最值,然后利用導數分析單調性,進而求最值。
”,于是整個問題就化為求函數的最值,然后利用導數分析單調性,進而求最值。
試題解析:由已知函數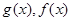 的定義域均為
的定義域均為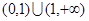 ,且
,且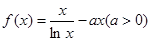 .
.
(1)函數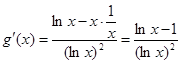 , 2分
, 2分
因f(x)在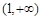 上為減函數,故
上為減函數,故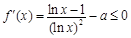 在
在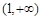 上恒成立.
上恒成立.
所以當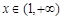 時,
時,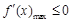 .
.
又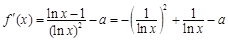
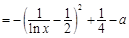 ,
,
故當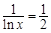 ,即
,即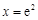 時,
時, .
.
所以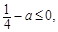 于是
于是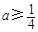 ,故a的最小值為
,故a的最小值為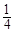 . 6分
. 6分
(2)命題“若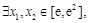 使
使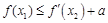 成立”等價于 “當
成立”等價于 “當 時,有
時,有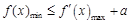 ”.
”.
由(Ⅱ),當 時,
時, ,
,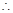
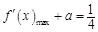 .
.
問題等價于:“當 時,有
時,有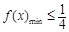 ”. 8分
”. 8分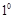 當
當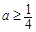 時,由(Ⅱ),
時,由(Ⅱ),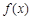 在
在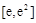 上為減函數,
上為減函數,
則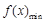 =
=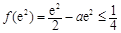 ,故
,故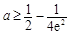 . 10分
. 10分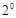 當
當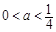 時,由于
時,由于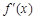
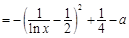 在
在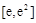 上為增函數,
上為增函數,
故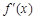 的值域為
的值域為 ,即
,即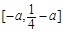 .
.
由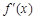 的單調性和值域知,
的單調性和值域知,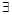 唯一
唯一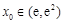 ,使
,使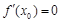 ,且滿足:
,且滿足:
當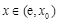 時,
時,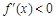 ,
,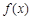 為減函數;
為減函數;
當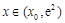 時,
時,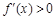 ,
,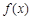 為增函數;
為增函數;
所以,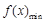 =
=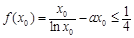 ,
,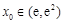 .
.
所以, ,與
,與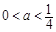 矛盾,不合題意. 11分
矛盾,不合題意. 11分
綜上,得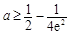 . 12分
. 12分
考點:1.導數公式;2.函數的單調性;3.恒成立問題;4.函數的最值以及命題的等價變換.


科目:高中數學 來源: 題型:解答題
為了降低能損耗,最近上海對新建住宅的屋頂和外墻都要求建造隔熱層.某幢建筑物要建造可使用20年的隔熱層,每厘米厚的隔熱層建造成本為6萬元.該建筑物每年的能消耗費用C(單位:萬元)與隔熱層厚度x(單位:cm)滿足關系:C(x)=(0≤x≤10),若不建隔熱層,每年能消耗費用為8萬元.設f(x)為隔熱層建造費用與20年的能消耗費用之和.
(1)求k的值及f(x)的表達式;
(2)隔熱層修建多厚時,總費用f(x)達到最小,并求最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
設函數 ,
, ,其中實數
,其中實數 .
.
(1)若 ,求函數
,求函數 的單調區間;
的單調區間;
(2)當函數 與
與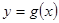 的圖象只有一個公共點且
的圖象只有一個公共點且 存在最小值時,記
存在最小值時,記 的最小值為
的最小值為 ,求
,求 的值域;
的值域;
(3)若 與
與 在區間
在區間 內均為增函數,求實數
內均為增函數,求實數 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
設函數 ,
, ,其中實數
,其中實數 .
.
(1)若 ,求函數
,求函數 的單調區間;
的單調區間;
(2)當函數 與
與 的圖象只有一個公共點且
的圖象只有一個公共點且 存在最小值時,記
存在最小值時,記 的最小值為
的最小值為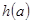 ,求
,求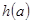 的值域;
的值域;
(3)若 與
與 在區間
在區間 內均為增函數,求實數
內均為增函數,求實數 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知函數 (
( 為常數,
為常數, 為自然對數的底)
為自然對數的底)
(1)當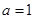 時,求
時,求 的單調區間;
的單調區間;
(2)若函數 在
在 上無零點,求
上無零點,求 的最小值;
的最小值;
(3)若對任意的 ,在
,在 上存在兩個不同的
上存在兩個不同的 使得
使得 成立,求
成立,求 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某投資公司年初用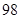 萬元購置了一套生產設備并即刻生產產品,已知與生產產品相關的各種配套費用第一年需要支出
萬元購置了一套生產設備并即刻生產產品,已知與生產產品相關的各種配套費用第一年需要支出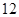 萬元,第二年需要支出
萬元,第二年需要支出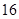 萬元,第三年需要支出
萬元,第三年需要支出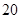 萬元,……,每年都比上一年增加支出
萬元,……,每年都比上一年增加支出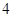 萬元,而每年的生產收入都為
萬元,而每年的生產收入都為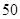 萬元.假設這套生產設備投入使用
萬元.假設這套生產設備投入使用 年,
年,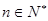 ,生產成本等于生產設備購置費與這
,生產成本等于生產設備購置費與這 年生產產品相關的各種配套費用的和,生產總利潤
年生產產品相關的各種配套費用的和,生產總利潤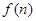 等于這
等于這 年的生產收入與生產成本的差. 請你根據這些信息解決下列問題:
年的生產收入與生產成本的差. 請你根據這些信息解決下列問題:
(Ⅰ)若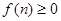 ,求
,求 的值;
的值;
(Ⅱ)若干年后,該投資公司對這套生產設備有兩個處理方案:
方案一:當年平均生產利潤取得最大值時,以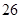 萬元的價格出售該套設備;
萬元的價格出售該套設備;
方案二:當生產總利潤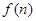 取得最大值時,以
取得最大值時,以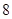 萬元的價格出售該套設備. 你認為哪個方案更合算?請說明理由.
萬元的價格出售該套設備. 你認為哪個方案更合算?請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com