
已知向量 =
= ,
,  =
=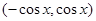 ,
,  =
=
(1)若 ,求向量
,求向量 、
、 的夾角
的夾角
(2)當 時,求函數
時,求函數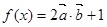 的最大值
的最大值
 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:解答題
已知 為坐標原點,
為坐標原點,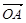 =(
=( ),
),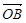 =(1,
=(1, ),
),  .
.
(1)若 的定義域為[-
的定義域為[- ,
,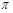 ],求y=
],求y= 的單調遞增區間;
的單調遞增區間;
(2)若 的定義域為[
的定義域為[ ,
,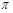 ],值域為[2,5],求
],值域為[2,5],求 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知A(-1,0),B(0,2),C(-3,1), ·
· ="5,"
="5,"  =10.
=10.
(1)求D點的坐標.
(2)若D點在第二象限,用 ,
, 表示
表示 .
.
(3)設 =(m,2),若3
=(m,2),若3 +
+ 與
與 垂直,求
垂直,求 的坐標.
的坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
平面直角坐標系xOy內有向量 =(1,7),
=(1,7), =(5,1),
=(5,1), =(2,1),點Q為直線OP上一動點.
=(2,1),點Q為直線OP上一動點.
(1)當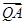 ·
· 取得最小值時,求
取得最小值時,求 坐標;
坐標;
(2)當點Q滿足(1)中條件時,求cos∠AQB的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com