分析:(1)求出函數的定義域,根據函數是奇函數,f(x)+f(-x)=0對x∈(-1,1)恒成立,可構造關于p的方程,進而求出p的值;
(2)根據(1)可得函數f(x)的解析式,進而根據關于x0的方程,解方程可得x0的值;
(3)根據(1)可得函數f(x)的解析式,構造關于x的不等式,解不等式可得x的取值范圍.
解答:解:(1)若函數的解析式有意義
,
則函數f(x)的定義域為(-1,1)…(2分)
因為f(x)是奇函數,
所以f(x)+f(-x)=0對x∈(-1,1)恒成立,
log
2(1-x)+plog
2(1+x)+log
2(1+x)+plog
2(1-x)=0對x∈(-1,1)恒成立,
即(p+1)[log
2(1-x)+log
2(1+x)]=0對x∈(-1,1)恒成立,
即(p+1)log
2(1-x
2)=0對x∈(-1,1)恒成立,
故p+1=0
所以p=-1.…(6分)
(2)由(1)可得f(x)=log
2(1-x)-log
2(1+x),
則
f()+f()=log
2(1-
)-log
2(1+
)+log
2(1-
)-log
2(1+
)
=log
2(
)-log
2(
)+log
2(
)-log
2(
)
=log
2(
÷
×
÷
)=log
2(
)
f(x
0)=log
2(1-x
0)-log
2(1+x
0)=log
2(
),
故
=
解方程得
x0=…(10分)
(3)f(x)=log
2(1-x)-log
2(1+x),
則f(x)>2等價于
>4,
解得:
-1<x<-,
所以x的取值范圍是
-1<x<-.…(14分)
點評:本題考查的知識點是對數函數的圖象與性質的綜合應用,函數奇偶性的性質,對數的運算性質,其中根據已知求出函數f(x)的解析式是解答本題的關鍵.



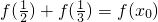 ,求x0的值;
,求x0的值; ,求x的值;
,求x的值;