
已知函數 ,
, .
.
(1)若函數 在
在 上不具有單調性,求實數
上不具有單調性,求實數 的取值范圍;
的取值范圍;
(2)若 .
.
(ⅰ)求實數 的值;
的值;
(ⅱ)設 ,
, ,
, ,當
,當 時,試比較
時,試比較 ,
, ,
, 的大小.
的大小.
(1)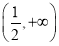 (2)(ⅰ)2(ⅱ)
(2)(ⅰ)2(ⅱ)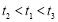
【解析】
試題分析:將二次函數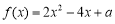 的解析式進行配方,根據其開口方向的對稱軸得到該函數的單調區間, 函數
的解析式進行配方,根據其開口方向的對稱軸得到該函數的單調區間, 函數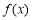 在
在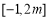 上不具有單調性,說明二次函數的對稱軸在區間
上不具有單調性,說明二次函數的對稱軸在區間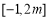 內,由此便可求出的取值范圍;
內,由此便可求出的取值范圍;
(2)(ⅰ)由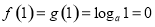 建立方程可解實數
建立方程可解實數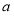 的值;
的值;
(ⅱ)分別根據二次函數、對數函數、指數函數的性質求出當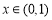 時,
時,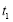 ,
,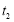 ,
,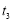 各自的取值范圍,進而比較它們的大小.
各自的取值范圍,進而比較它們的大小.
試題解析:【解析】
(1)∵拋物線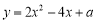 開口向上,對稱軸為
開口向上,對稱軸為 ,
,
∴函數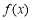 在
在 單調遞減,在
單調遞減,在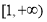 單調遞增, 2分
單調遞增, 2分
∵函數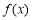 在
在 上不單調
上不單調
∴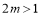 ,得
,得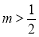 ,
,
∴實數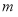 的取值范圍為
的取值范圍為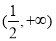 5分
5分
(2)(ⅰ)∵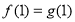 ,
,
∴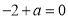
∴實數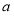 的值為
的值為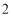 . 8分
. 8分
(ⅱ)∵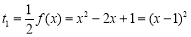 , 9分
, 9分
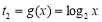 ,
,
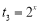 ,
,
∴當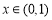 時,
時,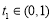 ,
,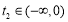 ,
,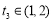 , 12分
, 12分
∴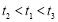 . 13分
. 13分
考點:二次函數、指數函數、對數函數的性質.


 教材全解字詞句篇系列答案
教材全解字詞句篇系列答案科目:高中數學 來源:2016屆福建省高一上學期期中考試數學試卷(解析版) 題型:選擇題
若 ,則函數
,則函數 與
與 的圖象
的圖象
A. 關于直線y=x對稱 B. 關于x軸對稱
C. 關于y軸對稱 D. 關于原點對稱
查看答案和解析>>
科目:高中數學 來源:2016屆福建省高一上學期期末數學試卷(解析版) 題型:選擇題
設 是兩條不同的直線,
是兩條不同的直線, 是三個不同的平面,給出下列四個命題:
是三個不同的平面,給出下列四個命題:
①若 ,
, ,則
,則
②若 ,
, ,
, ,則
,則
③若 ,
, ,
, ,則
,則
④若 ,
, ,
, ,則
,則
正確命題的個數是( )
A.1 B.2 C.3 D.4
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com