
已知數列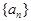 是等差數列,且
是等差數列,且 ,
, ,
,
(1)求數列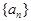 的通項公式; (2)令
的通項公式; (2)令 ,求數列
,求數列 前n項和
前n項和 .
.
(1)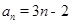 (2)
(2)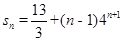
解析試題分析:解:(1)數列{an}是等差數列,且a1=1,a1+a2+a3=12,設出公差為d,∴a1+a1+d+a1+2d=12,∴a1+d=4,可得2+d=4,解得d=2,∴an=a1+(n-1)d=1+(n-1)×2=2n+1,(2)數列{an}的通項公式為an=n•2n,設其前n項和為Sn,∴Sn=1•21+2•22+3•23+…+n•2n①
2Sn=1•22+2•23+3•24+…+n•2n+1②
①-②可得-Sn=21+22+23+…+2n-n•2n+1②
∴-Sn=-2+22+23++…+2n -n•2n+1,
∴Sn=n×2n+1-2n+1+2=(n-1)2n+1+2;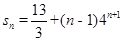
考點:等差數列,數列的求和
點評:主要是考查了等差數列的定義,以及通項公式的運用,以及錯位相減法來求解數列的和,屬于中檔題。


 名校課堂系列答案
名校課堂系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com