
(1) 給定正整數(shù)n![]() 5,集合 An=
5,集合 An=![]() .是否存在一一映射
.是否存在一一映射 ![]() : An
: An![]() An滿足條件:對一切k ( 1
An滿足條件:對一切k ( 1![]() k
k ![]() n-1 ) , 都有k |
n-1 ) , 都有k | ![]() (1)+
(1)+![]() (2) +……+
(2) +……+![]() (k) ?
(k) ?
(2) N* 為全體正整數(shù)的集合,是否存在一一映射 ![]() : N*
: N*![]() N* 滿足條件:對一切k
N* 滿足條件:對一切k![]() N*, 都有k |
N*, 都有k | ![]() (1)+
(1)+![]() (2) + ……+
(2) + ……+![]() (k) ?
(k) ?
證明你的結(jié)論 .
注: 映射 ![]() : A
: A![]() B 稱為一一映射,如果對任意 b
B 稱為一一映射,如果對任意 b![]() B,有且只有一個 a
B,有且只有一個 a![]() A 使得
A 使得 ![]() (a)=b . 題中“|”為整除符號.
(a)=b . 題中“|”為整除符號.
解析:(1) 不存在. ( 5 分)記 S k =![]() .當(dāng) n = 2m+1 時 ( m
.當(dāng) n = 2m+1 時 ( m ![]() 2 ), 由 2m | S 2 m 及S 2 m=
2 ), 由 2m | S 2 m 及S 2 m=![]() -
-![]() (2m+1) 得
(2m+1) 得 ![]() (2m+1)
(2m+1)![]() m+1(mod 2m), 但
m+1(mod 2m), 但 ![]() (2m+1)
(2m+1)![]() A 2m+1,故
A 2m+1,故![]() (2m+1)= m+1.再由 2m-1 | S2m-1及
(2m+1)= m+1.再由 2m-1 | S2m-1及
S2m-1=![]() -(m+1)-
-(m+1)-![]() (2m) 得
(2m) 得![]() (2m)
(2m) ![]() m+1(mod 2m-1),又有
m+1(mod 2m-1),又有![]() (2m)= m+1,與
(2m)= m+1,與![]()
的一一性矛盾. ( 5 分)
當(dāng) n = 2m+2 時 ( m![]() 2 ), S2m+1=
2 ), S2m+1=![]() -
-![]() (2m+2) 給出
(2m+2) 給出![]() (2m+2)=1 或 2m+2,
(2m+2)=1 或 2m+2,
同上又得![]() (2m+1)=
(2m+1)= ![]() (2m)= m+2 或 m+1 ,矛盾. ( 5 分)
(2m)= m+2 或 m+1 ,矛盾. ( 5 分)
(2) 存在. 對n 歸納定義![]() (2n-1)及
(2n-1)及![]() (2n) 如下: ( 5 分)
(2n) 如下: ( 5 分)
令![]()
![]() (1)=1,
(1)=1, ![]() (2)=3 .設(shè)已定義出不同的正整數(shù)值
(2)=3 .設(shè)已定義出不同的正整數(shù)值![]() (k) (1
(k) (1![]() k
k![]() 2n)滿足整除條件且包含 1,2,…,n ,設(shè) v 是未取到的最小正整數(shù)值,由于 2n+1 與 2n+2 互素,根據(jù)孫子定理,存在不同于v及
2n)滿足整除條件且包含 1,2,…,n ,設(shè) v 是未取到的最小正整數(shù)值,由于 2n+1 與 2n+2 互素,根據(jù)孫子定理,存在不同于v及![]() (k) (1
(k) (1![]() k
k![]() 2n)的正整數(shù)u滿足同余式組
2n)的正整數(shù)u滿足同余式組
u![]() -S2n(mod 2n+1)
-S2n(mod 2n+1)![]() -S2n-v (mod 2n+2) . ( 5 分)
-S2n-v (mod 2n+2) . ( 5 分)
定義![]() (2n+1)=u,
(2n+1)=u, ![]() (2n+2)=v .則正整數(shù)
(2n+2)=v .則正整數(shù)![]() (k) ( 1
(k) ( 1![]() k
k![]() 2n+2 )也互不相同,滿足整除條件,且包含
2n+2 )也互不相同,滿足整除條件,且包含
1,2,…,n+1 .根據(jù)數(shù)學(xué)歸納法原理,已經(jīng)得到符合要求的一一映射



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
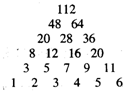 給定正整數(shù)n(n≥2)按圖方式構(gòu)成三角形數(shù)表:第一行依次寫上數(shù)1,2,3,…,n,在下面一行的每相鄰兩個數(shù)的正中間上方寫上這兩個數(shù)之和,得到上面一行的數(shù)(比下一行少一個數(shù)),依此類推,最后一行(第n行)只有一個數(shù).例如n=6時數(shù)表如圖所示,則當(dāng)n=2010時最后一行的數(shù)是
給定正整數(shù)n(n≥2)按圖方式構(gòu)成三角形數(shù)表:第一行依次寫上數(shù)1,2,3,…,n,在下面一行的每相鄰兩個數(shù)的正中間上方寫上這兩個數(shù)之和,得到上面一行的數(shù)(比下一行少一個數(shù)),依此類推,最后一行(第n行)只有一個數(shù).例如n=6時數(shù)表如圖所示,則當(dāng)n=2010時最后一行的數(shù)是查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
| n |
 |
| i-1 |
| n |
 |
| j-1 |
| a11 | a12 | … | a1n |
| a21 | a22 | … | a2n |
| … | … | … | … |
| an1 | an2 | … | ann |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com