
已知拋物線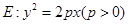 的準線與x軸交于點M,過點M作圓
的準線與x軸交于點M,過點M作圓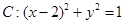 的兩條切線,切點為A、B,
的兩條切線,切點為A、B,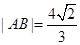 .
.
(1)求拋物線E的方程;
(2)過拋物線E上的點N作圓C的兩條切線,切點分別為P、Q,若P,Q,O(O為原點)三點共線,求點N的坐標.
(1)y2=4x;(2)點N坐標為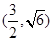 或
或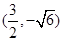 .
.
解析試題分析:本題主要考查拋物線的標準方程及其幾何性質、圓的標準方程及其幾何性質、圓的切線的性質等基礎知識,考查學生分析問題解決問題的能力和計算能力.第一問,利用拋物線的準線,得到M點的坐標,利用圓的方程得到圓心C的坐標,在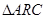 中,可求出
中,可求出 ,在
,在 中,利用相似三角形進行角的轉換,得到
中,利用相似三角形進行角的轉換,得到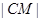 的長,而
的長,而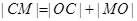 ,從而解出P的值,即得到拋物線的標準方程;第二問,設出N點的坐標,利用N、C點坐標寫出圓C的方程,利用點C的坐標寫出圓C的方程,兩方程聯立,由于P、Q是兩圓的公共點,所以聯立得到的方程即為直線PQ的方程,而O點在直線上,代入點O的坐標,即可得到s、t的值,即得到N點坐標.
,從而解出P的值,即得到拋物線的標準方程;第二問,設出N點的坐標,利用N、C點坐標寫出圓C的方程,利用點C的坐標寫出圓C的方程,兩方程聯立,由于P、Q是兩圓的公共點,所以聯立得到的方程即為直線PQ的方程,而O點在直線上,代入點O的坐標,即可得到s、t的值,即得到N點坐標.
試題解析:(1)由已知得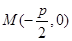 ,C(2,0).
,C(2,0).
設AB與x軸交于點R,由圓的對稱性可知,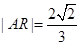 .
.
于是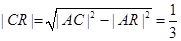 ,
,
所以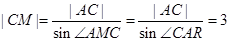 ,即
,即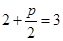 ,p=2.
,p=2.
故拋物線E的方程為y2=4x. 5分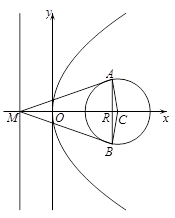
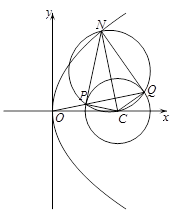
(2)設N(s,t).
P,Q是NC為直徑的圓D與圓C的兩交點.
圓D方程為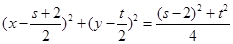 ,
,
即x2+y2-(s+2)x-ty+2s=0. ①
又圓C方程為x2+y2-4x+3=0. ②
②-①得(s-2)x+ty+3-2s=0. ③ 9分
P,Q兩點坐標是方程①和②的解,也是方程③的解,從而③為直線PQ的方程.
因為直線PQ經過點O,所以3-2s=0,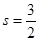 .
.
故點N坐標為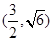 或
或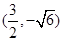 . 12分
. 12分
考點:拋物線的標準方程及其幾何性質、圓的標準方程及其幾何性質、圓的切線的性質.


 活力課時同步練習冊系列答案
活力課時同步練習冊系列答案科目:高中數學 來源: 題型:解答題
已知橢圓 的中心在原點
的中心在原點 ,焦點在
,焦點在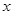 軸上,離心率為
軸上,離心率為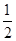 ,右焦點到右頂點的距離為
,右焦點到右頂點的距離為 .
.
(Ⅰ)求橢圓 的標準方程;
的標準方程;
(Ⅱ)是否存在與橢圓 交于
交于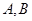 兩點的直線
兩點的直線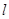 :
: ,使得
,使得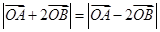 成立?若存在,求出實數
成立?若存在,求出實數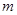 的取值范圍,若不存在,請說明理由.
的取值范圍,若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
設橢圓 的中心和拋物線
的中心和拋物線 的頂點均為原點
的頂點均為原點 ,
, 、
、 的焦點均在
的焦點均在 軸上,過
軸上,過 的焦點F作直線
的焦點F作直線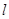 ,與
,與 交于A、B兩點,在
交于A、B兩點,在 、
、 上各取兩個點,將其坐標記錄于下表中:
上各取兩個點,將其坐標記錄于下表中: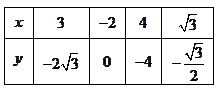

(1)求 ,
, 的標準方程;
的標準方程;
(2)若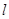 與
與 交于C、D兩點,
交于C、D兩點,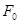 為
為 的左焦點,求
的左焦點,求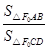 的最小值;
的最小值;
(3)點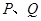 是
是 上的兩點,且
上的兩點,且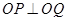 ,求證:
,求證: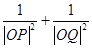 為定值;反之,當
為定值;反之,當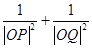 為此定值時,
為此定值時,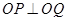 是否成立?請說明理由.
是否成立?請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知橢圓 的離心率
的離心率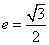 ,連接橢圓的四個頂點得到的菱形的面積為4.
,連接橢圓的四個頂點得到的菱形的面積為4.
(1)求橢圓的方程;
(2)設直線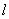 與橢圓相交于不同的兩點
與橢圓相交于不同的兩點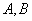 ,已知點
,已知點 的坐標為
的坐標為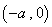 ,點
,點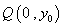 在線段
在線段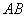 的垂直平分線上,且
的垂直平分線上,且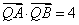 ,求
,求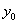 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知橢圓C: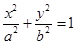 (a>b>0),過點(0,1),且離心率為
(a>b>0),過點(0,1),且離心率為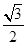 .
.
(1)求橢圓C的方程;
(2)A,B為橢圓C的左右頂點,直線l:x=2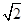 與x軸交于點D,點P是橢圓C上異于A,B的動點,直線AP,BP分別交直線l于E,F兩點.證明:當點P在橢圓C上運動時,
與x軸交于點D,點P是橢圓C上異于A,B的動點,直線AP,BP分別交直線l于E,F兩點.證明:當點P在橢圓C上運動時,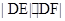 恒為定值.
恒為定值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
我們將不與拋物線對稱軸平行或重合且與拋物線只有一個公共點的直線稱為拋物線的切線,這個公共點稱為切點.解決下列問題:
已知拋物線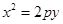
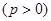 上的點
上的點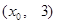 到焦點的距離等于4,直線
到焦點的距離等于4,直線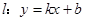 與拋物線相交于不同的兩點
與拋物線相交于不同的兩點 、
、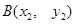 ,且
,且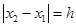 (
(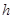 為定值).設線段
為定值).設線段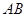 的中點為
的中點為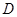 ,與直線
,與直線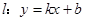 平行的拋物線的切點為
平行的拋物線的切點為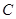 ..
..
(1)求出拋物線方程,并寫出焦點坐標、準線方程;
(2)用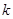 、
、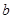 表示出
表示出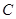 點、
點、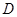 點的坐標,并證明
點的坐標,并證明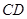 垂直于
垂直于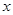 軸;
軸;
(3)求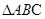 的面積,證明
的面積,證明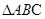 的面積與
的面積與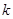 、
、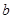 無關,只與
無關,只與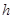 有關.
有關.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知點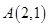 在拋物線
在拋物線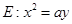 上,直線
上,直線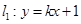 (
( ,且
,且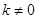 )與拋物線
)與拋物線 ,相交于
,相交于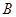 、
、 兩點,直線
兩點,直線 、
、 分別交直線
分別交直線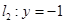 于點
于點 、
、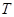 .
.
(1)求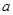 的值;
的值;
(2)若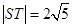 ,求直線
,求直線 的方程;
的方程;
(3)試判斷以線段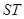 為直徑的圓是否恒過兩個定點?若是,求這兩個定點的坐標;若不是,說明理由.
為直徑的圓是否恒過兩個定點?若是,求這兩個定點的坐標;若不是,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
巳知橢圓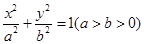 的離心率是
的離心率是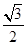 .
.
⑴若點P(2,1)在橢圓上,求橢圓的方程;
⑵若存在過點A(1,0)的直線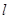 ,使點C(2,0)關于直線
,使點C(2,0)關于直線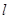 的對稱點在橢圓上,求橢圓的焦距的取值范圍.
的對稱點在橢圓上,求橢圓的焦距的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知橢圓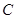 :
: 的離心率為
的離心率為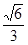 ,右焦點為(
,右焦點為( ,0).
,0).
(1)求橢圓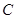 的方程;
的方程;
(2)若過原點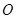 作兩條互相垂直的射線,與橢圓交于
作兩條互相垂直的射線,與橢圓交于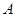 ,
,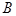 兩點,求證:點
兩點,求證:點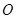 到直線
到直線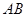 的距離為定值.
的距離為定值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com