已知函數(shù)
f(x)=2sin2+sinx-+1.
(Ⅰ)求
f()的值;
(Ⅱ)求f(x)的單調遞增區(qū)間;
(Ⅲ)作出f(x)在一個周期內的圖象.
(Ⅰ)由已知
f()=2sin2+sin-+1…(2分)
=
+-+1=1.…(4分)
(Ⅱ)∵
f(x)=(1-cosx)+sinx-+1…(6分)
=
sinx-cosx+1=
2sin(x-)+1.…(7分)
∵函數(shù)y=sinx的單調遞增區(qū)間為
[2kπ-,2kπ+](k∈Z),…(8分)
由
2kπ-≤x-≤2kπ+,得
2kπ-≤x≤2kπ+.
所以f(x)的單調遞增區(qū)間為
[2kπ-,2kπ+](k∈Z).…(9分)
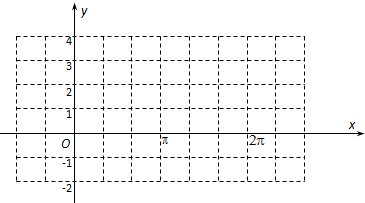
(Ⅲ)列表:
作出f(x)在一個周期
[,]上的圖象如圖所示.…(12分)

練習冊系列答案
相關習題
科目:高中數(shù)學
來源:不詳
題型:解答題
函數(shù)
y=Asin(ωx+φ)(A>0,ω>0,-<φ<)的圖象相鄰的最高點與最低點的坐標分別為
(,3),(,-3),求函數(shù)解析式.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
已知函數(shù)f(x)=Asin(ωx+
)(其中A>0,ω>0)的振幅為2,周期為π.
(Ⅰ)求f(x)的解析式;
(Ⅱ)求f(x)的單調增區(qū)間.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
已知函數(shù)f(x)=3cos(
+
)
(1)求出f(x)的最小正周期、單調增區(qū)間、對稱軸方程;
(2)說明此函數(shù)圖象可由y=cosx上的圖象經怎樣的變換得到.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
將函數(shù)f(x)=sin2x+cos2x的圖象向左平移
個單位得到函數(shù)y=g(x)的圖象,則函數(shù)y=g(x)的圖象
( )
| A.關于直線x=對稱 | B.關于直線x=對稱 |
| C.關于點(-,0)對稱 | D.關于點(,0)對稱 |
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
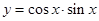
是( ).
| A.奇函數(shù) |
| B.偶函數(shù) |
| C.既是奇函數(shù)也是偶函數(shù) |
| D.既不是奇函數(shù)也不是偶函數(shù) |
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
已知

,則

的值等于( )
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
已知函數(shù)

(1)將

寫成

的形式,并求其圖象對稱中心的橫坐標;
(2)如果△ABC的三邊

滿足

,且邊

所對的角為

,試求

的范圍及此時函數(shù)

的值域.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
已知
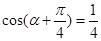
,則
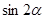
的值為 ( ).
查看答案和解析>>





 第1卷單元月考期中期末系列答案
第1卷單元月考期中期末系列答案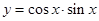 是( ).
是( ).
 寫成
寫成 的形式,并求其圖象對稱中心的橫坐標;
的形式,并求其圖象對稱中心的橫坐標; 滿足
滿足 ,且邊
,且邊 所對的角為
所對的角為 ,試求
,試求 的范圍及此時函數(shù)
的范圍及此時函數(shù) 的值域.
的值域.