中文字幕人妻色偷偷久久-精品久久久久成人码免费动漫-久久精品国产清自在天天线-国产成人精品免高潮在线观看

精英家教網 > 高中數學 > 題目詳情

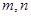已知是正整數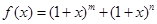，的展開式中的系數為7.求展開式中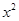的系數的最小值，并求這時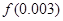的近似值（精確到0.01）．

的系數最小值為9，此時的近似值為.

解析試題分析：先利用二項展開式的通項公式求出的展開式中的的系數，進而由條件得到，然后再得到的系數，進而轉化成，根據二次函數的圖像與性質可確定或時的系數最小，進而根據二項展開式可確定此時的近似值.
由已知可得，則展開式中的系數為

所以當或時的系數最小為
這時，
.
考點：二項式定理.

練習冊系列答案
相關習題

科目：高中數學 來源： 題型：解答題

已知的第五項的二項式系數與第三項的二項式系數的比是，
(1)求n；
(2)求展開式中常數項．

查看答案和解析>>

科目：高中數學 來源： 題型：解答題

已知的展開式的二項式系數的和比(3x－1)n的展開式的二項式系數和大992,求(2x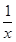－)2n的展開式中，(1)二項式系數最大的項；(2)系數的絕對值最大的項．

查看答案和解析>>

科目：高中數學 來源： 題型：解答題

有6名男醫生，4名女醫生．
(1)選3名男醫生，2名女醫生，讓這5名醫生到5個不同地區去巡回醫療，共有多少種不同方法？
(2)把10名醫生分成兩組，每組5人且每組都要有女醫生，則有多少種不同分法？若將這兩組醫生分派到兩地去，并且每組選出正副組長兩人，又有多少種不同方案？

查看答案和解析>>

科目：高中數學 來源： 題型：解答題

由數字1、2、3、4、5、6組成無重復數字的數中，求：
（1）六位偶數的個數；
（2）求三個偶數互不相鄰的六位數的個數；
（3）求恰有兩個偶數相鄰的六位數的個數；
（4）奇數字從左到右，從小到大依次排列的六位數的個數．

查看答案和解析>>

科目：高中數學 來源： 題型：解答題

已知(＋3x2)n的展開式中，各項系數和比它的二項式系數和大992，求：
(1)展開式中二項式系數最大的項；
(2)展開式中系數最大的項．

查看答案和解析>>

科目：高中數學 來源： 題型：解答題

某醫院有內科醫生12名，外科醫生8名，現選派5名參加賑災醫療隊，其中
(1)某內科醫生甲與某外科醫生乙必須參加，共有多少種不同選法？
(2)甲、乙均不能參加，有多少種選法？
(3)甲、乙兩人至少有一人參加，有多少種選法？
(4)隊中至少有一名內科醫生和一名外科醫生，有幾種選法？

查看答案和解析>>

科目：高中數學 來源： 題型：解答題

已知的展開式前三項中的的系數成等差數列.
（1）求展開式中所有的的有理項；（2）求展開式中系數最大的項.

查看答案和解析>>

科目：高中數學 來源： 題型：填空題

展開式中不含項的系數的和為                      .

查看答案和解析>>

同步練習冊答案