
如圖,已知四棱錐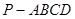 中,底面
中,底面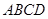 是直角梯形,
是直角梯形,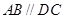 ,
,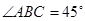 ,
,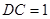 ,
,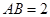 ,
,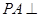 平面
平面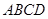 ,
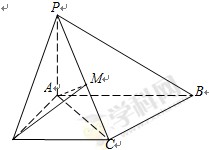
,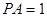 .
. 
(Ⅰ)求證: 平面
平面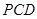 ;
;
(Ⅱ)求證: 平面
平面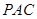 ;
;
(Ⅲ)若 是
是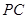 的中點(diǎn),求三棱錐
的中點(diǎn),求三棱錐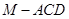 的體積.
的體積.
 全能測控一本好卷系列答案
全能測控一本好卷系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:解答題
如圖,在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AB=5,AA1=4,點(diǎn)D是AB的中點(diǎn).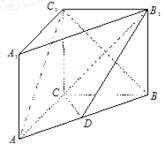
(1)求證: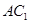 ∥平面
∥平面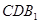 ;
;
(2)求異面直線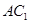 與
與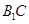 所成角的余弦值.
所成角的余弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
如圖,在四棱錐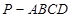 中,底面為直角梯形,
中,底面為直角梯形,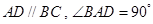 ,
, 垂直于底面
垂直于底面 ,
, 分別為
分別為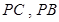 的中點(diǎn).
的中點(diǎn).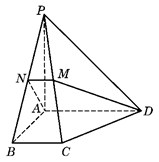
(1)求證: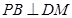 ;
;
(2)求點(diǎn)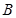 到平面
到平面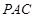 的距離.
的距離.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
將邊長為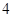 的正方形
的正方形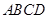 和等腰直角三角形
和等腰直角三角形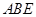 按圖拼為新的幾何圖形,
按圖拼為新的幾何圖形,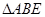 中,
中,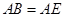 ,連結(jié)
,連結(jié)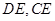 ,若
,若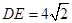 ,
,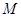 為
為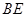 中點(diǎn)
中點(diǎn)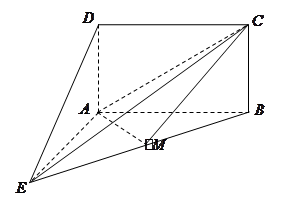
(Ⅰ)求 與
與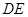 所成角的大小;
所成角的大小;
(Ⅱ)若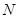 為
為 中點(diǎn),證明:
中點(diǎn),證明: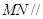 平面
平面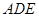 ;
;
(Ⅲ)證明:平面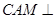 平面
平面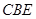
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
如圖,在三棱錐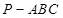 中,
中,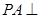 平面
平面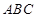 ,
,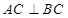 ,
,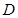 為側(cè)棱
為側(cè)棱 上一點(diǎn),它的正(主)視圖和側(cè)(左)視圖如圖所示.
上一點(diǎn),它的正(主)視圖和側(cè)(左)視圖如圖所示.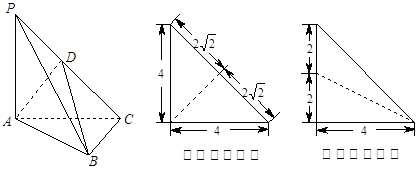
(1)證明: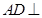 平面
平面 ;
;
(2)在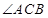 的平分線上確定一點(diǎn)
的平分線上確定一點(diǎn) ,使得
,使得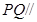 平面
平面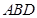 ,并求此時(shí)
,并求此時(shí)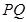 的長.
的長.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
如圖,在三棱柱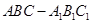 中,側(cè)面
中,側(cè)面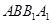 ,
,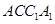 均為正方形,∠
均為正方形,∠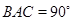 ,點(diǎn)
,點(diǎn)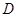 是棱
是棱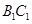 的中點(diǎn).
的中點(diǎn).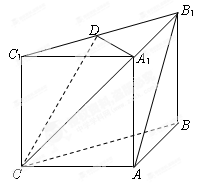
(Ⅰ)求證: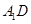 ⊥平面
⊥平面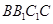 ;
;
(Ⅱ)求證: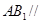 平面
平面 ;
;
(Ⅲ)求二面角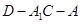 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
如圖,在長方體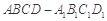 ,中,
,中,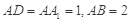 ,點(diǎn)
,點(diǎn) 在棱AB上移動(dòng).
在棱AB上移動(dòng).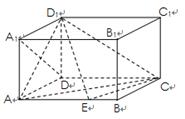
(Ⅰ)證明: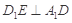 ;
;
(Ⅱ)求點(diǎn)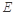 到平面
到平面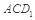 的距離;
的距離;
(Ⅲ)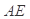 等于何值時(shí),二面角
等于何值時(shí),二面角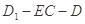 的大小為
的大小為
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
如圖,在四棱錐 中,底面
中,底面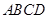 為菱形,
為菱形,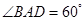 ,
,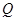 為
為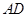 的中點(diǎn).
的中點(diǎn).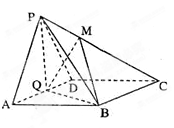
(1)若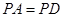 ,求證:平面
,求證:平面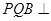 平面
平面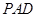 ;
;
(2)點(diǎn)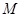 在線段
在線段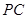 上,
上,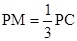 ,若平面
,若平面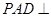 平面
平面 ,且
,且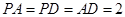 ,求二面角
,求二面角 的大小.
的大小.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
如圖所示,在正方體ABCD﹣A1B1C1D1中,棱長AB=1.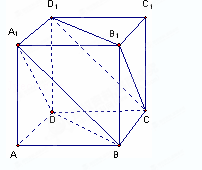
(Ⅰ)求異面直線A1B與 B1C所成角的大小;(Ⅱ)求證:平面A1BD∥平面B1CD1.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com