甲、乙兩容器中分別盛有兩種濃度的某種溶液
，從甲容器中取出
溶液，將其倒入乙容器中攪勻，再從乙容器中取出溶液，將其倒入甲容器中攪勻，這稱為是一次調(diào)和，已知第一次調(diào)和后，甲、乙兩種溶液的濃度分別記為：
，
，第
次調(diào)和后的甲、乙兩種溶液的濃度分別記為：
、
.
（1）請用、
分別表示和
；
（2）問經(jīng)過多少次調(diào)和后，甲乙兩容器中溶液的濃度之差小于
.
（1）
，
；（2）
.
解析試題分析：（1）根據(jù)題中條件歸納出第
次調(diào)和時乙容器中溶質(zhì)的量
等于從甲容器中取出的溶質(zhì)的量
以及從乙容器中本身的溶質(zhì)的量
之和，從而得到與和之間的關(guān)系，利用同樣的方法得到
與與，從而實現(xiàn)利用和來表示；（2）利用（1）中的表達式并結(jié)合定義得到數(shù)列
為等比數(shù)列，求出該數(shù)列的首項與公比，確定數(shù)列的通項公式，然后解不等式
，求出相應(yīng)的即可.
（1）由題意可設(shè)在第一次調(diào)和后的濃度為，，
；
（2）由于題目中的問題是針對濃度之差，所以，我們不妨直接考慮數(shù)列．
由（1）可得：
，
所以，數(shù)列是以
為首項，以
為公比的等比數(shù)列．
所以，
，
由題，令，得
．所以，
，
由
得
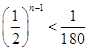，所以，
.
即第次調(diào)和后兩溶液的濃度之差小于.
考點：1.遞推數(shù)列；2.指數(shù)不等式
寒假樂園北京教育出版社系列答案科目：高中數(shù)學(xué) 來源： 題型：解答題
設(shè)
為數(shù)列
的前
項和，對任意的
N，都有
為常數(shù)，且
．
（1）求證：數(shù)列是等比數(shù)列；
（2）設(shè)數(shù)列的公比
與
函數(shù)關(guān)系為
，數(shù)列
滿足
，點
落在 上，
，N，求數(shù)列
的通項公式；
（3）在滿足（2）的條件下，求數(shù)列
的前項和
，使
恒成立時，求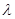
的最小值．[
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：解答題
某地今年年初有居民住房面積為
m2，其中需要拆除的舊房面積占了一半，當?shù)赜嘘P(guān)部門決定每年以當年年初住房面積的10%的住房增長率建設(shè)新住房，同時每年拆除xm2的舊住房，又知該地區(qū)人口年增長率為4.9‰．
（1）如果10年后該地區(qū)的人均住房面積正好比目前翻一番，那么每年應(yīng)拆除的舊住房面積x是多少？
（2）依照（1）拆房速度，共需多少年能拆除所有需要拆除的舊房？
下列數(shù)據(jù)供計算時參考：
| 1.19=2.38 | 1.00499=1.04 |
| 1.110=2.6 | 1.004910=1.05 |
| 1.111=2.85 | 1.004911=1.06 |
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：解答題
已知等比數(shù)列
首項為
，公比為q,求（1）該數(shù)列的前n項和
。
（2）若q≠1，證明數(shù)列 
不是等比數(shù)列
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：解答題
已知等比數(shù)列
中，
，前
項和是前
項中所有偶數(shù)項和的
倍．
（1）求通項
；
（2）已知
滿足
，若是遞增數(shù)列，求實數(shù)
的取值范圍．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：解答題
已知數(shù)列
的前
項和為
滿足
（ 
）
（1）證明數(shù)列
為等比數(shù)列；
（2）設(shè)
，求數(shù)列
的前項和
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：解答題
在數(shù)列{an}中，a1＝2，an＋1＝4an－3n＋1，n∈N*.
(1)求證：數(shù)列{an－n}是等比數(shù)列；
(2)求數(shù)列{an}的前n項和Sn；
(3)求證：不等式Sn＋1≤4Sn對任意n∈N*皆成立．
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
中，
，公比
，
為
，求數(shù)列
的通項公式．