
已知函數(shù)
(1)若對任意的 恒成立,求實數(shù)
恒成立,求實數(shù) 的最小值.
的最小值.
(2)若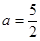 且關于
且關于 的方程
的方程 在
在 上恰有兩個不相等的實數(shù)根,求實數(shù)
上恰有兩個不相等的實數(shù)根,求實數(shù) 的取值范圍;
的取值范圍;
(3)設各項為正的數(shù)列 滿足:
滿足: 求證:
求證:
(1) ; (2)
; (2)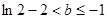 ; (3)
; (3)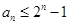
【解析】
試題分析:(I)依題意,對任意的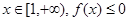 恒成立,即
恒成立,即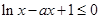 在x
在x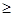 1恒成立.則a
1恒成立.則a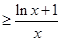 .
.
而
 0,所以,
0,所以,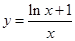 在
在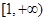 是減函數(shù),
是減函數(shù),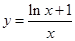 最大值為1,所以,
最大值為1,所以,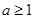 ,實數(shù)
,實數(shù) 的最小值。
的最小值。
(II)因為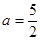 ,且
,且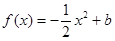 在
在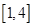 上恰有兩個不相等的實數(shù)根,
上恰有兩個不相等的實數(shù)根,
即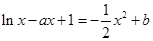 在
在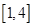 上恰有兩個不相等的實數(shù)根,
上恰有兩個不相等的實數(shù)根,
設g(x)=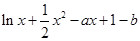 ,則g'(x)=
,則g'(x)=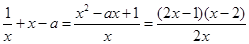
列表:
|
X |
(0, |
|
( |
2 |
(2,4) |
|
|
+ |
0 |
- |
0 |
+ |
|
|
增函數(shù) |
極大值 |
減函數(shù) |
極小值 |
增函數(shù) |
所以,g(x)極大值=g(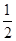 )=
)= -ln2-b,g(x)極大值=g(2)=ln2-b-2,
-ln2-b,g(x)極大值=g(2)=ln2-b-2,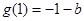 ,g(4)=2ln2-b-1
,g(4)=2ln2-b-1
因為,方程g(x)=0在[1,4]上恰有兩個不相等的實數(shù)根.
則 ,解得
,解得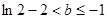 .
.
(III)設h(x)=lnx-x+1,x∈[1,+∞),則h'(x)= -1≤0
-1≤0
∴h(x)在[1,+∞)為減函數(shù),且h(x)max=h(1)=0,故當x≥1時有l(wèi)nx≤x-1.
∵a1=1,假設ak≥1(k∈N*),則ak+1=lnak+ak+2>1,故an≥1(n∈N*)
從而an+1=lnan+an+2≤2an+1∴1+an+1≤2(1+an)≤…≤2n(1+a1)
即1+an≤2n,∴an≤2n-1
考點:本題主要考查應用導數(shù)研究函數(shù)的單調性及極(最)值,研究函數(shù)的圖象和性質,數(shù)列不等式的證明。
點評:難題,不等式恒成立問題,常常轉化成求函數(shù)的最值問題。(II)(III)兩小題,均是通過構造函數(shù),研究函數(shù)的單調性、極值(最值),認識函數(shù)圖象的變化形態(tài)等,尋求得到解題途徑。有一定技巧性,對學生要求較高。


 一課四練系列答案
一課四練系列答案 黃岡小狀元滿分沖刺微測驗系列答案
黃岡小狀元滿分沖刺微測驗系列答案 新輔教導學系列答案
新輔教導學系列答案 陽光同學一線名師全優(yōu)好卷系列答案
陽光同學一線名師全優(yōu)好卷系列答案科目:高中數(shù)學 來源:2015屆河南靈寶三中高一上第三質檢數(shù)學試卷(解析版) 題型:解答題
(本小題滿分12分)已知函數(shù)
(1)若 對一切實數(shù)x恒成立,求實數(shù)a的取值范圍。
對一切實數(shù)x恒成立,求實數(shù)a的取值范圍。
(2)求 在區(qū)間
在區(qū)間 上的最小值
上的最小值 的表達式。
的表達式。
查看答案和解析>>
科目:高中數(shù)學 來源:2013屆江蘇省無錫市高二下期中數(shù)學試卷(成志班)(解析版) 題型:解答題
已知函數(shù)
(1)若對任意的 恒成立,求實數(shù)
恒成立,求實數(shù)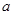 的最小值.
的最小值.
(2)若 且關于
且關于 的方程
的方程 在
在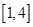 上恰有兩個不相等的實數(shù)根,求實數(shù)
上恰有兩個不相等的實數(shù)根,求實數(shù) 的取值范圍;
的取值范圍;
(3)設各項為正的數(shù)列 滿足:
滿足: 求證:
求證:
查看答案和解析>>
科目:高中數(shù)學 來源:2011-2012學年安徽省高三10月月考理科數(shù)學試卷 題型:解答題
(本題滿分12分)已知函數(shù) .
.
(1)若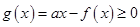 對任意
對任意 恒成立,求實數(shù)
恒成立,求實數(shù) 的取值范圍;
的取值范圍;
(2)若函數(shù) 的圖像與直線
的圖像與直線 有且僅有三個公共點,且公共點的橫坐標的最大值為
有且僅有三個公共點,且公共點的橫坐標的最大值為 ,求證:
,求證: .
.
查看答案和解析>>
科目:高中數(shù)學 來源:2013屆新疆烏魯木齊八中高二上學期期末考試理科數(shù)學 題型:解答題
已知函數(shù) .
.
(1)若對任意的實數(shù) ,都有
,都有 ,求
,求 的取值范圍;
的取值范圍;
(2)當 時,
時,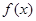 的最大值為M,求證:
的最大值為M,求證: ;
;
(3)若 ,求證:對于任意的
,求證:對于任意的 ,
, 的充要條件是
的充要條件是
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com