給定數列a1,a2,…,an.對i=1,2,…,n-1,該數列前i項的最大值記為Ai,后n-i項ai+1,ai+2,…,an的最小值記為Bi,di=Ai-Bi.
(Ⅰ)設數列{an}為3,4,7,1,寫出d1,d2,d3的值;
(Ⅱ)設a1,a2,…,an-1(n≥4)是公比大于1的等比數列,且a1>0.證明:d1,d2,…,dn-1是等比數列;
(Ⅲ)設d1,d2,…,dn-1是公差大于0的等差數列,且d1>0.證明:a1,a2,…,an-1是等差數列.
【答案】
分析:(Ⅰ)當i=1時,A
1=3,B
1=1,從而可求得d
1,同理可求得d
2,d
3的值;
(Ⅱ)依題意,可知a
n=a
1q
n-1(a
1>0,q>1),由d
k=a
k-a
k+1⇒d
k-1=a
k-1-a
k(k≥2),從而可證

(k≥2)為定值.
(Ⅲ)依題意,0<d
1<d
2<…<d
n-1,可用反證法證明a
1,a
2,…,a
n-1是單調遞增數列;再證明a
m為數列{a
n}中的最小項,從而可求得是a
k=d
k+a
m,問題得證.
解答:解:(Ⅰ)當i=1時,A
1=3,B
1=1,故d
1=A
1-B
1=2,同理可求d
2=3,d
3=6;
(Ⅱ)由a
1,a
2,…,a
n-1(n≥4)是公比q大于1的等比數列,且a
1>0,則{a
n}的通項為:a
n=a
1q
n-1,且為單調遞增的數列.
于是當k=1,2,…n-1時,d
k=A
k-B
k=a
k-a
k+1,
進而當k=2,3,…n-1時,

=
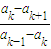
=
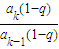
=q為定值.
∴d
1,d
2,…,d
n-1是等比數列;
(Ⅲ)若d
1,d
2,…,d
n-1是公差大于0的等差數列,則0<d
1<d
2<…<d
n-1.
先證明a
1,a
2,…,a
n-1是單調遞增數列.
否則設a
k是第一個使得a
k≤a
k-1成立的項,則A
k-1=A
k,B
k-1≤B
k,因此d
k-1=A
k-1-B
k-1≥A
k-B
k=d
k,矛盾.
因此a
1,a
2,…,a
n-1是單調遞增數列…①
再證明a
m為數列{a
n}中的最小項,否則設a
k<a
m(k=1,2,…n-1),顯然k≠1,否則d
1=A
1-B
1=a
1-B
1≤a
1-a
1=0,與d
1>0矛盾;
因而k≥2,此時考慮d
k-1=A
k-1-B
k-1=a
k-1-a
k<0,矛盾.
因此a
m為數列{a
n}中的最小項,…②
綜合①②d
k=A
k-B
k=a
k-a
m(k=1,2,…n-1),于是a
k=d
k+a
m,也即a
1,a
2,…,a
n-1是等差數列.
點評:本題考查等差數列與等比數列的綜合,突出考查考查推理論證與抽象思維的能力,考查反證法的應用,屬于難題.

 (k≥2)為定值.
(k≥2)為定值. =
=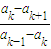 =
=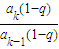 =q為定值.
=q為定值.

 科學實驗活動冊系列答案
科學實驗活動冊系列答案