空間四邊形ABCD中,E、F、G、H分別是AB、BC、CD、DA的中點,若AC=BD=a,且AC與BD所成的角為60°,則四邊形EFGH的面積是________.
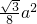
分析:先證明四邊形EFGH為菱形,然后說明∠EFG=60°,最后根據三角形的面積公式即可求出所求.
解答:連接EH,因為EH是△ABD的中位線,所以EH∥BD,且EH=BD.

同理,FG∥BD,EF∥AC,且FG=BD,EF=AC.
所以EH∥FG,且EH=FG.
所以四邊形EFGH為平行四邊形.
因為AC=BD=a,AC與BD所成的角為60°
所以EF=EH.所以四邊形EFGH為菱形,∠EFG=60°.
∴四邊形EFGH的面積是2×

×

=
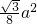
故答案為:
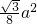
點評:主要考查知識點:簡單幾何體和公理四,公理四:和同一條直線平行的直線平行,證明菱形常用方法是先證明它是平行四邊形再證明鄰邊相等相等,以及面積公式屬于基礎題.

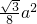

 ×
× =
=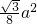
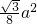


 如圖,已知空間四邊形ABCD中,BC=AC,AD=BD,E是AB的中點.
如圖,已知空間四邊形ABCD中,BC=AC,AD=BD,E是AB的中點.