
 ,B產品的利潤y2與投資金額x的函數關系為y2=
,B產品的利潤y2與投資金額x的函數關系為y2= (注:利潤與投資金額單位:萬元).
(注:利潤與投資金額單位:萬元). ;(2) 分別用20萬元和80萬元資金投資A、B兩種金融產品,可以使公司獲得最大利潤,最大利潤為28萬元.
;(2) 分別用20萬元和80萬元資金投資A、B兩種金融產品,可以使公司獲得最大利潤,最大利潤為28萬元.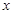 萬元資金投入
萬元資金投入 產品,利潤
產品,利潤 萬元;
萬元; 萬元資金投入
萬元資金投入 產品,利潤
產品,利潤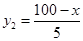 ,由
,由 可得所求函數關系;
可得所求函數關系;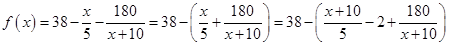
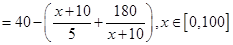 可考慮用基本不等式法求其最大值,并注意等號成立的條件。
可考慮用基本不等式法求其最大值,并注意等號成立的條件。 +
+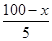
 -
- (x∈[0,100]). 6分
(x∈[0,100]). 6分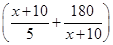 ,x∈[0,100],
,x∈[0,100],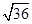 =28,取等號當且僅當
=28,取等號當且僅當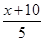 =
= 時,即x=20. 12分
時,即x=20. 12分

科目:高中數學 來源:不詳 題型:解答題
 內單調遞減,求a的取值范圍;
內單調遞減,求a的取值范圍;查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
 是奇函數,(其中
是奇函數,(其中 )
)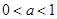 時,討論函數f(x)的增減性;
時,討論函數f(x)的增減性; 時,f(x)的值域是(1,
時,f(x)的值域是(1, ),求n與a的值。
),求n與a的值。查看答案和解析>>
科目:高中數學 來源:不詳 題型:單選題
A. | B.[-1,0] | C.(-∞,-2] | D. |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com