
A. | B.[-1,0] | C.(-∞,-2] | D. |
 海淀黃岡名師導航系列答案
海淀黃岡名師導航系列答案 普通高中同步練習冊系列答案
普通高中同步練習冊系列答案 優翼小幫手同步口算系列答案
優翼小幫手同步口算系列答案科目:高中數學 來源:不詳 題型:解答題
 ,B產品的利潤y2與投資金額x的函數關系為y2=
,B產品的利潤y2與投資金額x的函數關系為y2= (注:利潤與投資金額單位:萬元).
(注:利潤與投資金額單位:萬元).查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
 的定義域為
的定義域為 ,且
,且 的圖象連續不間斷. 若函數
的圖象連續不間斷. 若函數 滿足:對于給定的
滿足:對于給定的 (
( 且
且 ),存在
),存在 ,使得
,使得 ,則稱
,則稱 具有性質
具有性質 .
. ,
, ,判斷
,判斷 是否具有性質
是否具有性質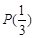 ,并說明理由;
,并說明理由; 若
若 具有性質
具有性質 ,求
,求 的最大值;
的最大值; 的定義域為
的定義域為 ,且
,且 的圖象連續不間斷,又滿足
的圖象連續不間斷,又滿足 ,
, 且
且 ,函數
,函數 具有性質
具有性質 .
.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com