中文字幕人妻色偷偷久久-精品久久久久成人码免费动漫-久久精品国产清自在天天线-国产成人精品免高潮在线观看

精英家教網 > 高中數學 > 題目詳情
給出下列命題
①存在，使；
②存在區間（a，b），使y=cosx為減函數而sinx＜0；
③y=tanx在其定義域內為增函數；
④既有最大值和最小值，又是偶函數；
⑤的最小正周期為π．
其中錯誤的命題為    （把所有符合要求的命題序號都填上）
【答案】分析：①由已知可得sinxcosx=＜0，則當x∈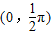不符合題意；②結合正弦函數與余弦函數的圖象可知，不存在區間使y=cosx為減函數而sinx＜0；③y=tanx在區間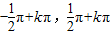（），（k∈Z）上單調遞增，但是在定義域內不是增函數；④=cos2x+cosx=-，可判斷函數的最值的情況，及函數的奇偶性⑤結合函數的圖象可知，的最小正周期為π．
解答：解：①若，則有1+2sinxcosx=，即sinxcosx=＜0，則當x∈不符合題意，故①錯誤
②結合正弦函數與余弦函數的圖象可知，不存在區間使y=cosx為減函數而sinx＜0；故②錯誤
③y=tanx在（），k∈Z上單調遞增，但是在定義域內不是增函數；故③錯誤
④=cos2x+cosx=-，當cosx=-時，函數有最小值，當cosx=1時，函數有最大值，從而可知函數既有最大值和最小值，又f（-x）=cos2（-x）+cos（-x）=cos2x+cosx=f（x），可得函數是偶函數；故④正確
⑤結合函數的圖象可知，不是周期函數．故⑤錯誤
故答案為：①②③⑤
點評：本題主要考查了函數的性質的綜合應用，解題的關鍵是熟練掌握函數的基本性質、常見的結論，并能靈活應用
練習冊系列答案
相關習題

科目：高中數學 來源： 題型：

給出下列命題
①存在x∈(0，
π
2
)，使sinx+cosx=
1
3
；
②存在區間（a，b），使y=cosx為減函數而sinx＜0；
③y=tanx在其定義域內為增函數；
④y=cos2x+sin(
π
2
-x)既有最大值和最小值，又是偶函數；
⑤y=sin|2x+
π
6
|的最小正周期為π．
其中錯誤的命題為
①②③⑤
①②③⑤
（把所有符合要求的命題序號都填上）

查看答案和解析>>

科目：高中數學 來源： 題型：

給出下列命題:

①存在實數α,使sinαcosα=1;

②存在實數α,使sinα+cosα=;

③y=sin(-2x)是偶函數;

④x=是函數y=sin(2x+)的一條對稱軸方程;

⑤若α、β是第一象限角，且α＞β，則tanα＞tanβ.其中正確命題的序號是_________.(注:把你認為正確的命題的序號都填上)

查看答案和解析>>

科目：高中數學 來源： 題型：

給出下列命題:

①存在實數α，使sinα·cosα=1成立；

②存在實數α，使sinα+cosα=成立；

③函數y=sin(-2x)是偶函數；

④方程x=是函數y=sin(2x+)圖象的一條對稱軸方程；

⑤若α、β是第一象限角，且α＞β，則tanα＞tanβ.

其中正確命題的序號是__________________.（注:把你認為正確的命題的序號都填上）

查看答案和解析>>

科目：高中數學 來源： 題型：

給出下列命題:

①存在實數α,使sinα·cosα=1成立；

②存在實數α,使sinα+cosα=成立；

③函數y=sin(-2x)是偶函數；

④方程x=是函數y=sin(2x+)圖象的一條對稱軸方程；

⑤若α、β是第一象限角，且α＞β,則tanα＞tanβ.

其中正確命題的序號是_______________.（注:把你認為正確的命題的序號都填上）

查看答案和解析>>

同步練習冊答案