
(���}�M��12��)
���c(di��n)��(-5,0)��(5,0)����һ�l�u������ ���p�����ķ��̣�
���p�����ķ��̣�
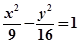
����ԇ�}�������O(sh��)�p�����ķ��̞�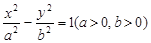 ,������������2��
,������������2��
��u������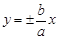 ,��������������������������������������.4��
,��������������������������������������.4��
�F(xi��n)��֪�p������һ�l�u������ ,��
,��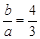 ,����.6��
,����.6��
���p������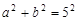 ,����������������������������������8��
,����������������������������������8��
���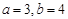 ,����������������������������������������������..10��
,����������������������������������������������..10��
���p�����ķ��̞�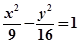 ����������������������..12��
����������������������..12��
���c(di��n)���p�������̼����|(zh��)
�c(di��n)�u(p��ng)�����c(di��n)��x�S�r(sh��)�u������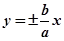 �����c(di��n)��y�S�r(sh��)�u������
�����c(di��n)��y�S�r(sh��)�u������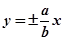



| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
(���}�M��13��)
��֪�E�A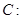
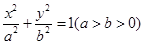 ���x���ʞ�
���x���ʞ�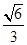 ���E�A���S�L(zh��ng)��
���E�A���S�L(zh��ng)��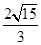 .
.
������E�A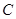 �ķ��̣�
�ķ��̣�
������֪?ji��ng)�ֱ��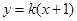 �c�E�A
�c�E�A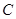 �ཻ��
�ཻ��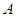 ��
��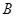 ���c(di��n). ��������
���c(di��n). ��������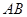 ���c(di��n)�ęM����(bi��o)��
���c(di��n)�ęM����(bi��o)��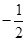 ����б��
����б��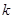 ��ֵ�������c(di��n)
��ֵ�������c(di��n)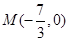 �����C��
�����C��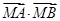 �鶨ֵ��
�鶨ֵ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
(��С�}�M��12�֣�
��1����ֱ�� ���p����
���p���� �صõ����L(zh��ng)��
�صõ����L(zh��ng)��
��2�����^���c(di��n) ��ֱ�����p����
��ֱ�����p���� �صõ������c(di��n)܉�E���̡�
�صõ������c(di��n)܉�E���̡�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
����С�}�M��12�֣�
����ɂ�(g��)�E�A���x������ȣ���ô�ͷQ�@�ɂ�(g��)�E�A����.��֪�E�A �c�E�A
�c�E�A ���ƣ��ҙE�A
���ƣ��ҙE�A ��һ��(g��)���S���c(di��n)�ǒ��タ
��һ��(g��)���S���c(di��n)�ǒ��タ �Ľ��c(di��n).
�Ľ��c(di��n).
����ԇ��E�A �Ę�(bi��o)��(zh��n)���̣�
�Ę�(bi��o)��(zh��n)���̣�
�����O(sh��)�E�A ��������ԭ�c(di��n)����(du��)�Q�S������(bi��o)�S�ϣ�ֱ��
��������ԭ�c(di��n)����(du��)�Q�S������(bi��o)�S�ϣ�ֱ�� �c�E�A
�c�E�A ����
���� ���c(di��n)�����c�E�A
���c(di��n)�����c�E�A ����
���� ���c(di��n).������
���c(di��n).������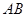 �c����
�c���� �����c(di��n)�غϣ�ԇ�Д��E�A
�����c(di��n)�غϣ�ԇ�Д��E�A �c�E�A
�c�E�A �Ƿ�����ƙE�A�����C������Д�.
�Ƿ�����ƙE�A�����C������Д�.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
�����}�M��13�֣�
�O(sh��)�c(di��n)P�LjAx2 +y2 =4������һ�c(di��n)�����c(di��n)P��x�S������PP0�������Po���� ��
��
�������c(di��n)M��܉�EC�ķ��̣�
�����O(sh��)ֱ�� ��y=kx+m(m��0)�c�����е�܉�EC���ڲ�ͬ�ă��c(di��n)A��B��
��y=kx+m(m��0)�c�����е�܉�EC���ڲ�ͬ�ă��c(di��n)A��B��
��1����ֱ��OA��AB��OB��б�ʳɵȱȔ�(sh��)�У���(sh��)��(sh��)m��ȡֵ������
��2������AB��ֱ���ĈA�^����C�cx�S�����S�Ľ��c(di��n)Q�����C��ֱ�� �^���c(di��n)(Q�c(di��n)����)�������ԓ���c(di��n)������(bi��o)��
�^���c(di��n)(Q�c(di��n)����)�������ԓ���c(di��n)������(bi��o)��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
����С�}�M��12�֣���֪�E�A�Ľ��c(di��n)����(bi��o)��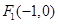 ��
��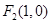 ���Ҷ��Sһ��c(di��n)B�M��
���Ҷ��Sһ��c(di��n)B�M��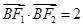 ��
��
���� ��E�A�ķ��̣�
�����^ ��ֱ��l�c�E�A���ڲ�ͬ�ă��c(di��n)M��N���t��
��ֱ��l�c�E�A���ڲ�ͬ�ă��c(di��n)M��N���t��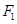 MN�ă�(n��i)�ЈA����e�Ƿ�������ֵ������������@��(g��)���ֵ���˕r(sh��)��ֱ�����̣��������ڣ�Ո(q��ng)�f�����ɡ�
MN�ă�(n��i)�ЈA����e�Ƿ�������ֵ������������@��(g��)���ֵ���˕r(sh��)��ֱ�����̣��������ڣ�Ո(q��ng)�f�����ɡ�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
(���}�M��14��)
��֪�E�A
 ,�����(zh��n)����
,�����(zh��n)���� ���Ҝ�(zh��n)����
���Ҝ�(zh��n)���� �����タ
�����タ ������(bi��o)ԭ�c(di��n)
������(bi��o)ԭ�c(di��n) ����c(di��n)��
����c(di��n)�� ���(zh��n)����
���(zh��n)���� ��
�� ��
�� ���c(di��n).
���c(di��n).
��1�����タ �Ę�(bi��o)��(zh��n)���̣�
�Ę�(bi��o)��(zh��n)���̣�
��2���� ���L(zh��ng)��.
���L(zh��ng)��.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
(���}�M��13��) ��D�� ���x���ʞ�
���x���ʞ�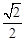 �ęE�A,
�ęE�A, ��
��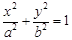 (
(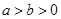 )�����ҽ��c(di��n)��ֱ��
)�����ҽ��c(di��n)��ֱ��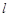 ��
��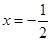 ������
������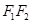 �ֳɃɶΣ����L(zh��ng)��֮�Ȟ�1 : 3���O(sh��)
�ֳɃɶΣ����L(zh��ng)��֮�Ȟ�1 : 3���O(sh��)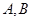 ��
��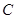 �ϵăɂ�(g��)��(d��ng)�c(di��n)������
�ϵăɂ�(g��)��(d��ng)�c(di��n)������ �����c(di��n)
�����c(di��n) ��ֱ��
��ֱ��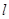 �ϣ�����
�ϣ����� ���д����c
������c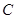 ����
����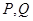 ���c(di��n)��
���c(di��n)��
(��) ��E�AC�ķ��̣�
(��) �Ƿ�����c(di��n) ��ʹ��
��ʹ�� ��ֱ���ĈA��(j��ng)�^�c(di��n)
��ֱ���ĈA��(j��ng)�^�c(di��n) �������ڣ����
�������ڣ���� �c(di��n)����(bi��o)���������ڣ�Ո(q��ng)�f�����ɣ�
�c(di��n)����(bi��o)���������ڣ�Ո(q��ng)�f�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
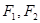 �քe�ǙE�A
�քe�ǙE�A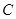 ��
��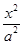 +
+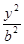 =1��
=1��
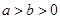 �������ҽ��c(di��n)��
�������ҽ��c(di��n)��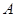 �ǙE�A
�ǙE�A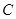 ������c(di��n)��
������c(di��n)��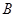 ��ֱ��
��ֱ��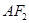 �c�E�A
�c�E�A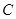 ����һ��(g��)���c(di��n)��
����һ��(g��)���c(di��n)��
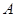
 =60��.
=60��.
��1����E�A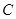 ���x���ʣ�
���x���ʣ�
��2����֪��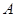
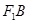 ����e��40
����e��40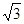 ����a, b ��ֵ.
����a, b ��ֵ.
�鿴�𰸺ͽ���>>
��(gu��)�H�W(xu��)У��(y��u)�x - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com