
已知數列 是首項為1,公差為
是首項為1,公差為 的等差數列,數列
的等差數列,數列 是首項為1,公比為
是首項為1,公比為 的等比
的等比
數列.
(1)若 ,
, ,求數列
,求數列 的前
的前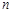 項和;
項和;
(2)若存在正整數 ,使得
,使得 .試比較
.試比較 與
與 的大小,并說明理由.
的大小,并說明理由.
(1) ;(2) 當
;(2) 當 時,
時,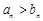 ;當
;當 時,
時,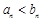 ;當
;當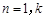 時,
時,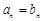 .
.
解析試題分析:(1)利用基本量思想求解兩個數列的通項公式,然后才有錯位相減法求解數列 的前
的前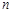 項和;(2)利用
項和;(2)利用 等量關系關系,減少公差d,進而將
等量關系關系,減少公差d,進而將 與
與 進行表示,然后才有作差比較進行分析,注意分類討論思想的應用.
進行表示,然后才有作差比較進行分析,注意分類討論思想的應用.
試題解析:(1)依題意,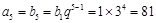 ,
,
故 ,
,
所以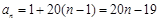 , 3分
, 3分
令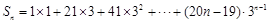 , ①
, ①
則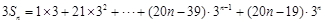 , ②
, ②
①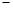 ②得,
②得,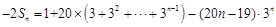 ,
,
 ,
,
所以 . 7分
. 7分
(2)因為 ,
,
所以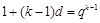 ,即
,即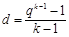 ,
,
故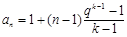 ,
,
又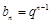 , 9分
, 9分
所以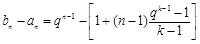
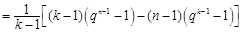
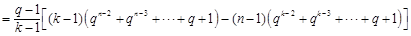
11分
(ⅰ)當 時,由
時,由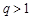 知
知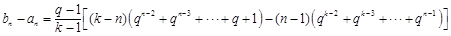
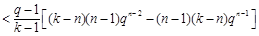
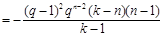
 , 13分
, 13分
(ⅱ)當 時,由
時,由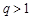 知
知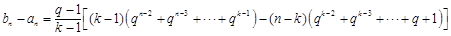
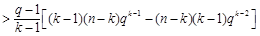
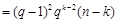
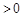 ,
,
綜上所述,當 時,
時,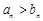 ;當
;當 時,
時,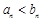 ;當
;當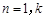 時,
時,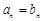 . 16分
. 16分
(注:僅給出“ 時,
時,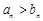 ;
; 時,
時,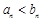 ”得2分.)
”得2分.)
方法二:(注意到數列的函數特征,運用函數性質求解)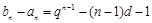 (易知
(易知 ),
),
令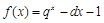 ,有
,有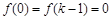 ,
, ,
,
令 ,則
,則 .記
.記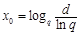 .
.
若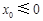 ,則在
,則在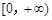 上
上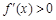 ,函數
,函數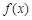 在
在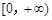 上為單調增函數,則
上為單調增函數,則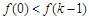


科目:高中數學 來源: 題型:解答題
已知數列 ,
,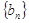 分別為等比,等差數列,數列
分別為等比,等差數列,數列 的前n項和為
的前n項和為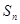 ,且
,且 ,
, ,
, 成等差數列,
成等差數列,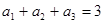 ,數列
,數列 中,
中,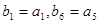 ,
,
(Ⅰ)求數列 ,
,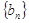 的通項公式;
的通項公式;
(Ⅱ)若數列 的前n項和為
的前n項和為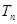 ,求滿足不等式
,求滿足不等式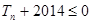 的最小正整數
的最小正整數 。
。
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知正項數列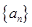 的首項
的首項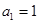 ,前
,前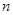 項和
項和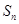 滿足
滿足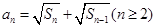 .
.
(Ⅰ)求證: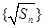 為等差數列,并求數列
為等差數列,并求數列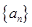 的通項公式;
的通項公式;
(Ⅱ)記數列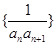 的前
的前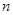 項和為
項和為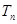 ,若對任意的
,若對任意的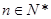 ,不等式
,不等式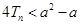 恒成立,求實數
恒成立,求實數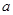 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
設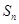 為數列
為數列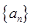 的前
的前 項和,對任意的
項和,對任意的 ,都有
,都有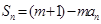 (
(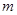 為正常數).
為正常數).
(1)求證:數列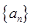 是等比數列;
是等比數列;
(2)數列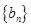 滿足
滿足 求數列
求數列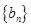 的通項公式;
的通項公式;
(3)在滿足(2)的條件下,求數列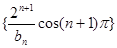 的前
的前 項和
項和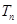 .
.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某市去年11份曾發生流感,據統計,11月1日該市新的流感病毒感染者有20人,此后,每天的新感染者平均比前一天的新感染者增加50人,由于該市醫療部門采取措施,使該種病毒的傳播得到控制,從某天起,每天的新感染者平均比前一天的新感染者減少30人,到11月30日止,該市在這30日內感染該病毒的患者總共8670人,問11月幾日,該市感染此病毒的新患者人數最多?并求這一天的新患者人數.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com