
(本小題滿分12分)已知 
(1)求 的最小值;
的最小值;
(2)求 的值域。
的值域。
(1) 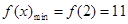 ; (2)
; (2) 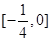 。
。
解析試題分析:(I)先根據 ,得到
,得到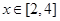 ,再結合二次函數的單調性可知f(x)在x=2處取得最小值。
,再結合二次函數的單調性可知f(x)在x=2處取得最小值。
(II)可以采用換元法令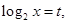 則
則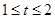 ,所以原函數可轉化為
,所以原函數可轉化為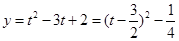 二次函數最值問題研究。
二次函數最值問題研究。
(1) ∵ 
∴ 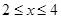 ……………………………………………………………2分
……………………………………………………………2分
又 在[2,4]上單調遞增………………………………3分
在[2,4]上單調遞增………………………………3分
所以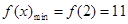 …………………………………………………5分
…………………………………………………5分
(2) ∵  =(
=(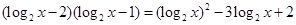
………………………………………………8分
設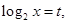 則
則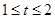
則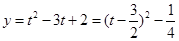 ……………………………………………10分
……………………………………………10分
所以可知當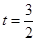 時,即
時,即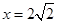 時,
時,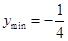
當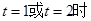 ,即
,即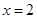 或4時,
或4時,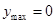
∴  的值域為
的值域為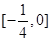 ……………………………12分
……………………………12分
考點:對數不等式,一元二次函數的最值,及換元法。
點評:掌握一元二次函數的性質是解本題的關鍵,其中知道對稱軸兩側單調性相同,對稱軸一側才具有單調性。


科目:高中數學 來源: 題型:解答題
(本小題12分)已知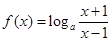 (
(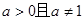 ).
).
(1)判斷函數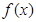 的奇偶性,并證明;
的奇偶性,并證明;
(2)若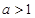 ,用單調性定義證明函數
,用單調性定義證明函數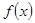 在區間
在區間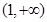 上單調遞減;
上單調遞減;
(3)是否存在實數 ,使得
,使得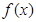 的定義域為
的定義域為 時,值域為
時,值域為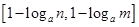 ,若存在,求出實數
,若存在,求出實數 的取值范圍;若不存在,則說明理由.
的取值范圍;若不存在,則說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題滿分12分)經市場調查,某種商品在過去50天的銷售量和價格均為銷售時間t(天)的函數,已知前30天價格為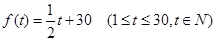 ,后20天價格為f(t)="45" (31£ t £50, tÎN),且銷售量近似地滿足g(t)=" -2t+200" (1£t£50, tÎN).
,后20天價格為f(t)="45" (31£ t £50, tÎN),且銷售量近似地滿足g(t)=" -2t+200" (1£t£50, tÎN).
(I)寫出該種商品的日銷售額S與時間t的函數關系式;
(II)求日銷售額S的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com