
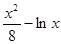 ,x∈[1,3],
,x∈[1,3],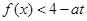 于任意的x∈[1,3],t∈[0,2]恒成立,求實數(shù)a的取值范圍.
于任意的x∈[1,3],t∈[0,2]恒成立,求實數(shù)a的取值范圍.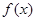 的最大值為
的最大值為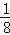 ,最小值為
,最小值為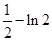 ;(2)
;(2)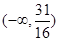 .
.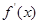 ,再求
,再求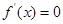 的根,再判斷根兩側導數(shù)的符號,進而判斷函數(shù)大致圖象,再從大致圖象并比較端點函數(shù)值的大小來確定最大值和最小值;(2)恒成立問題關鍵搞清變量和參數(shù)的關系,一般遵循“知道誰的范圍,誰是變量;求誰的范圍,誰是參數(shù)”的原則,該題中首先利用
的根,再判斷根兩側導數(shù)的符號,進而判斷函數(shù)大致圖象,再從大致圖象并比較端點函數(shù)值的大小來確定最大值和最小值;(2)恒成立問題關鍵搞清變量和參數(shù)的關系,一般遵循“知道誰的范圍,誰是變量;求誰的范圍,誰是參數(shù)”的原則,該題中首先利用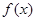 的最大值小于
的最大值小于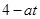 ,得關于
,得關于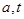 恒成立的不等式,再根據(jù)
恒成立的不等式,再根據(jù)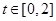 ,求參數(shù)
,求參數(shù)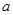 的范圍.
的范圍.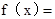
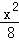
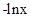 ,所以
,所以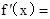
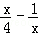 ,令
,令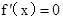 得
得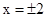 ,因為
,因為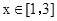 ,
,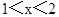 時
時 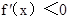 ;當
;當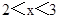 時,
時,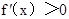 ;∴
;∴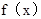 在
在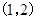 上單調(diào)減函數(shù),在
上單調(diào)減函數(shù),在 上單調(diào)增函數(shù),∴
上單調(diào)增函數(shù),∴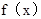 在
在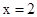 處取得極小值
處取得極小值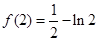 ; 又
; 又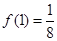 ,
,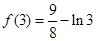 ,∵
,∵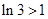 ∴
∴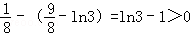 ∴
∴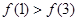 ,
,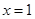 時
時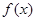 的最大值為
的最大值為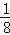 ,
,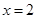 時函數(shù)取得最小值為
時函數(shù)取得最小值為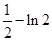 .
.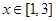 時,
時,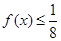 ,故對任意
,故對任意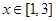 ,
,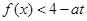 恒成立,
恒成立,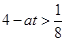 對任意
對任意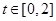 恒成立,即
恒成立,即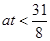 恒成立,記
恒成立,記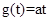 ,
,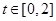
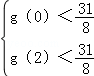 ,解得
,解得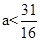 ,∴實數(shù)a的取值范圍是
,∴實數(shù)a的取值范圍是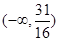 .
.

科目:高中數(shù)學 來源:不詳 題型:解答題
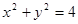 上任取一點
上任取一點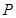 ,設點
,設點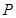 在
在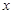 軸上的正投影為點
軸上的正投影為點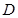 .當點
.當點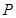 在圓上運動時,動點
在圓上運動時,動點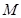 滿足
滿足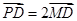 ,動點
,動點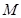 形成的軌跡為曲線
形成的軌跡為曲線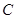 .
.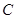 的方程;
的方程;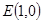 ,若
,若 、
、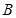 是曲線
是曲線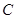 上的兩個動點,且滿足
上的兩個動點,且滿足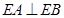 ,求
,求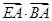 的取值范圍.
的取值范圍.查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:解答題
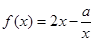 的定義域為
的定義域為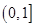 (a為實數(shù)),
(a為實數(shù)),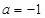 時,求函數(shù)
時,求函數(shù)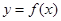 的值域。
的值域。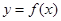 在定義域上是減函數(shù),求a的取值范圍
在定義域上是減函數(shù),求a的取值范圍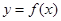 在
在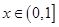 上的最大值及最小值。
上的最大值及最小值。查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:單選題
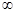 )上單調(diào)遞減的是( )
)上單調(diào)遞減的是( )| A.y=-ln|x| | B.y=x3 | C.y=2|x| | D.y=cosx |
查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:單選題
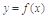 定義域為
定義域為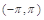 ,且函數(shù)
,且函數(shù)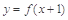 的圖象關于直線
的圖象關于直線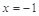 對稱,當
對稱,當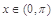 時,
時,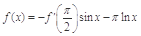 ,(其中
,(其中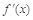 是
是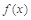 的導函數(shù)),若
的導函數(shù)),若 ,
,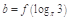 ,
,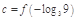 則
則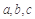 的大小關系是( )
的大小關系是( )A.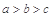 | B.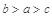 | C.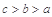 | D.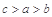 |
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com