
已知函數 的圖象關于原點對稱。
的圖象關于原點對稱。
(1)求m的值;(2)判斷 在
在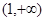 上的單調性,并根據定義證明。
上的單調性,并根據定義證明。
(1)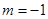 ;(2)當
;(2)當 時,
時,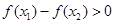 ,由函數單調性定義知
,由函數單調性定義知 在
在 上單調增;當
上單調增;當 時,
時,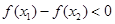 ,由函數單調性定義知
,由函數單調性定義知 在
在 上單調減。
上單調減。
解析試題分析:(1)由已知條件得 ------------2分
------------2分
即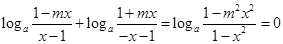 ,
,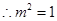 ,即
,即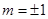 ------2分
------2分
當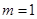 時,
時, 無意義,故
無意義,故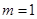 舍去
舍去
因此,只有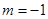 滿足題意-----------2分
滿足題意-----------2分
(2)由(1)知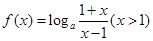 ,設
,設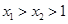
則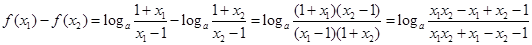
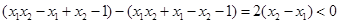 ,且
,且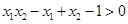 ,
, ,
,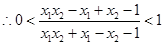 ------------4分
------------4分
當 時,
時,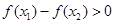 ,由函數單調性定義知
,由函數單調性定義知 在
在 上單調增
上單調增
當 時,
時,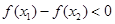 ,由函數單調性定義知
,由函數單調性定義知 在
在 上單調減
上單調減
-----------------3分
考點:函數的奇偶性;函數的單調性;用定義法證明函數的單調性。
點評:用定義法證明函數單調性的步驟:一設二作差三變形四判斷符號五得出結論,其中最重要的是四變形,最好變成幾個因式乘積的形式,這樣便于判斷符號。


 優等生題庫系列答案
優等生題庫系列答案 53天天練系列答案
53天天練系列答案科目:高中數學 來源: 題型:解答題
已知定義在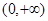 的函數
的函數 ,對任意的
,對任意的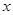 、
、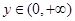 ,都有
,都有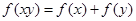 ,且當
,且當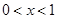 時,
時,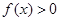 .
.
(1)證明:當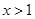 時,
時,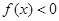 ;
;
(2)判斷函數 的單調性并加以證明;
的單調性并加以證明;
(3)如果對任意的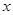 、
、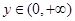 ,
,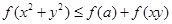 恒成立,求實數
恒成立,求實數 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
本小題滿分12分)
今有一長2米寬1米的矩形鐵皮,如圖,在四個角上分別截去一個邊長為x米的正方形后,沿虛線折起可做成一個無蓋的長方體形水箱(接口連接問題不考慮).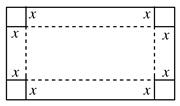
(Ⅰ)求水箱容積的表達式 ,并指出函數
,并指出函數 的定義域;
的定義域;
(Ⅱ)若要使水箱容積不大于 立方米的同時,又使得底面積最大,求x的值.
立方米的同時,又使得底面積最大,求x的值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本題滿分12分)已知某公司生產某品牌服裝的年固定成本為10萬元,每生產一千件,需要另投入2.7萬元.設該公司年內共生產該品牌服裝 千件并全部銷售完,每千件的銷售收入為
千件并全部銷售完,每千件的銷售收入為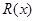 萬元,且
萬元,且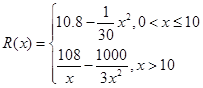 .
.
(I)寫出年利潤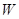 (萬元)關于年產量
(萬元)關于年產量 (千件)的函數關系式;
(千件)的函數關系式;
(Ⅱ)年生產量為多少千件時,該公司在這一品牌服裝的生產中所獲年利潤最大?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題滿分13分))
京廣高鐵于2012年12月26日全線開通運營,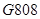 次列車在平直的鐵軌上勻速行駛,由于遇到緊急情況,緊急剎車時列車行駛的路程
次列車在平直的鐵軌上勻速行駛,由于遇到緊急情況,緊急剎車時列車行駛的路程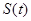 (單位:
(單位: )和時間
)和時間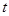 (單位:
(單位: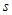 )的關系為:
)的關系為: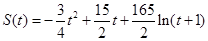 .
.
(1)求從開始緊急剎車至列車完全停止所經過的時間;
(2)求列車正常行駛的速度;
(3)求緊急剎車后列車加速度絕對值的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
有一批運動服裝原價為每套80元,兩個商場均有銷售,為了吸引顧客,兩商場紛紛推出優惠政策。甲商場的優惠辦法是:買一套減4元,買兩套每套減8元,買三套每套減12元,......,依此類推,直到減到半價為止;乙商場的優惠辦法是:一律7折。某單位欲為每位員工買一套運動服裝,問選擇哪個商場購買更省錢?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某汽車生產企業上年度生產一品牌汽車的投入成本為10萬元/輛,出廠價為13萬元/輛,年銷售量為5000輛.本年度為適應市場需求,計劃提高產品檔次,適當增加投入成本,若每輛車投入成本增加的比例為 (0<
(0< <1
<1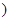 ,則出廠價相應提高的比例為0.7
,則出廠價相應提高的比例為0.7 ,年銷售量也相應增加.已知年利潤=(每輛車的出廠價-每輛車的投入成本)×年銷售量.
,年銷售量也相應增加.已知年利潤=(每輛車的出廠價-每輛車的投入成本)×年銷售量.
(1)若年銷售量增加的比例為0.4 ,為使本年度的年利潤比上年度有所增加,則投入成本增加的比例
,為使本年度的年利潤比上年度有所增加,則投入成本增加的比例 應在什么范圍內?
應在什么范圍內?
(2)年銷售量關于 的函數為
的函數為 ,則當
,則當 為何值時,本年度的年利潤最大?最大利潤為多少?
為何值時,本年度的年利潤最大?最大利潤為多少?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題滿分12分)定義在實數R上的函數y= f(x)是偶函數,當x≥0時,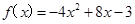 .
.
(Ⅰ)求f(x)在R上的表達式;
(Ⅱ)求y=f(x)的最大值,并寫出f(x)在R上的單調區間(不必證明).
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com