
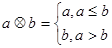 ,令
,令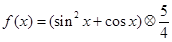 ,且
,且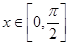 ,則函數
,則函數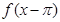 的最大值是( )
的最大值是( )A.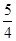 | B.1 | C.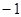 | D.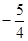 |
 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源:不詳 題型:解答題
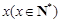 名員工從事第三產業,調整后他們平均每人每年創造利為
名員工從事第三產業,調整后他們平均每人每年創造利為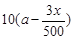 萬元
萬元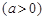 ,剩下的員工平均每人每年創造的利潤可以提高
,剩下的員工平均每人每年創造的利潤可以提高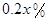 .
.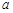 的取值范圍是多少?
的取值范圍是多少?查看答案和解析>>
科目:高中數學 來源:不詳 題型:單選題
| A.?x∈R,x2≥2014 | B.?x∈R,x2<2014 |
| C.?x∈R,x2≥2014 | D.?x∈R,x2>2014 |
查看答案和解析>>
科目:高中數學 來源:不詳 題型:填空題
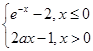 ,(a是常數且a>0).對于下列命題:
,(a是常數且a>0).對于下列命題: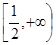 上恒成立,則a的取值范圍是a>1;
上恒成立,則a的取值范圍是a>1; 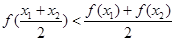
查看答案和解析>>
科目:高中數學 來源:不詳 題型:單選題
| A.y隨x的增大而增大 |
| B.不論x為何值,總有y>0 |
| C.必經過二、四象限 |
| D.圖象必經過點(0,5) |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com