中文字幕人妻色偷偷久久-精品久久久久成人码免费动漫-久久精品国产清自在天天线-国产成人精品免高潮在线观看

精英家教網 > 高中數學 > 題目詳情

如圖所示，已知平行六面體AC1的底面ABCD為菱形，且∠C1CB＝∠C1CD＝∠BCD．

(1)

求證：C1C⊥BD

(2)

當的值為多少時，能使A1C⊥平面C1BD?請給出證明

答案：
解析：

(1)

　　解：設=a，=b，=c則｜a｜=｜b｜．設、、兩兩所夾角為θ，于是=－=a－b．

　　·=c·(a－b)=c·a－c·b

　　　　　　 =｜c｜｜a｜cosθ－｜c｜｜b｜cosθ=0．

　　∴⊥即CC1⊥BD．

　　分析：由a⊥ba·b=0，若證兩向量垂直，只需證兩直線對應向量的數量積為0即可．

(2)

　　若使A1C⊥平面C1BD，只需使A1C⊥BD，A1C⊥DC1．

　　由·=(＋)·(－)

　　　　　　　 =(a＋b＋c)·(a－c)

　　　　　　　 =｜a｜2－｜c｜2＋｜a｜·｜b｜cosθ－｜b｜·｜c｜cosθ=0．

　　得當｜a｜=｜c｜時，A1C⊥DC1．

　　同理可證當｜a｜=｜c｜時，A1C⊥BD．

　　∴當=1時．A1C⊥平面C1BD．

　　點評：無垂直關系的立體幾何問題，也可以設空間的基向量a、b、c，利用向量的運算律解．


練習冊系列答案
相關習題

科目：高中數學 來源： 題型：

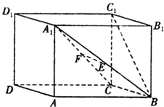精英家教網如圖所示，已知直平行六面體ABCD-A1B1C1D1的底面邊長均為2a，側棱長為a，∠ABC=60°，E、F分別是A1B、A1C的中點．
（1）求證：EF∥平面BB1CC1；
（2）求二面角A1-BC-A的大小．

查看答案和解析>>

科目：高中數學 來源：單元雙測　同步達標活頁試卷　高二數學(下A) 人教版 題型：047

如圖所示，已知平行六面體ABCD－A1B1C1D1的底面ABCD是菱形，且∠C1CB＝∠C1CD＝∠BCD＝

(1)

求證：C1C⊥BD

(2)

假定CD＝2，CC1＝，求二面角C1－BD－C的大小的大小

(3)

當的值為多少時，能使A1C⊥平面C1BD?請給出證明

查看答案和解析>>

科目：高中數學 來源： 題型：

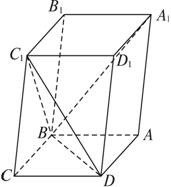
如圖所示，已知平行六面體ABCD—A1B1C1D1的底面是菱形，且∠C1CB=∠C1CD=∠BCD=60°.

(1)求證：CC1⊥BD;

(2)當的值為多少時，能使A1C⊥平面C1BD？并加以證明.

查看答案和解析>>

科目：高中數學 來源：同步題 題型：證明題

如圖所示，已知平行六面體ABCD-A1B1C1D1 的底面ABCD 是菱形，且∠C1CB= ∠C1CD= ∠BCD=60 °．     求證：CC1 ⊥BD.

查看答案和解析>>

同步練習冊答案