
已知數(shù)列 滿足
滿足 ,
, .
.
(1)令 ,證明:
,證明: 是等比數(shù)列;
是等比數(shù)列;
(2)求 的通項(xiàng)公式.
的通項(xiàng)公式.
(1)詳見解析;(2) .
.
解析試題分析:(1)要證明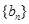 是等比數(shù)列,只需證明
是等比數(shù)列,只需證明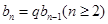 ,其中
,其中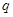 是不為零的常數(shù),因此,只需把
是不為零的常數(shù),因此,只需把 及
及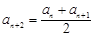 代入,即可得
代入,即可得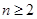 時,
時,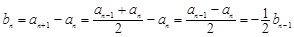 ,又由
,又由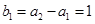 可得
可得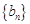 是首項(xiàng)為
是首項(xiàng)為 ,公比為
,公比為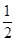 的等比數(shù)列,從而得證;(2)由(1)可得
的等比數(shù)列,從而得證;(2)由(1)可得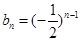 ,即有
,即有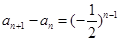 ,考慮采用累加法求其通項(xiàng)公式,即可得
,考慮采用累加法求其通項(xiàng)公式,即可得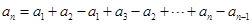
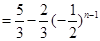 .
.
(1)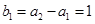 2分
2分
當(dāng)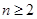 時,
時,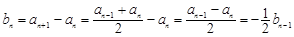 , 6分
, 6分
∴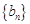 是首項(xiàng)為
是首項(xiàng)為 ,公比為
,公比為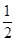 的等比數(shù)列; 8分
的等比數(shù)列; 8分
(2)由(1)可得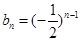 ,∴
,∴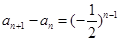 , 10分
, 10分
∴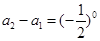 ,
,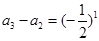 ,
,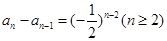 ,...............12分
,...............12分
∴ ,
,
當(dāng)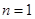 時,也符合,∴
時,也符合,∴ 16分
16分
考點(diǎn):1.等比數(shù)列的證明與前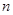 項(xiàng)和;2累加法求數(shù)列通項(xiàng)公式.
項(xiàng)和;2累加法求數(shù)列通項(xiàng)公式.


 名校練考卷期末沖刺卷系列答案
名校練考卷期末沖刺卷系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:解答題
已知等比數(shù)列 中,
中, ,
, ,
, ,
, 分別為△ABC的三個內(nèi)角A,B,C的對邊,且
分別為△ABC的三個內(nèi)角A,B,C的對邊,且 .
.
(1)求數(shù)列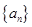 的公比
的公比 ;
;
(2)設(shè)集合 ,且
,且 ,求數(shù)列
,求數(shù)列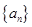 的通項(xiàng)公式.
的通項(xiàng)公式.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
某種平面分形圖如下圖所示,一級分形圖是由一點(diǎn)出發(fā)的三條線段,長度均為1,兩兩夾角為 ;二級分形圖是在一級分形圖的每條線段的末端出發(fā)再生成兩條長度為原來
;二級分形圖是在一級分形圖的每條線段的末端出發(fā)再生成兩條長度為原來 的線段,且這兩條線段與原線段兩兩夾角為
的線段,且這兩條線段與原線段兩兩夾角為 ;依此規(guī)律得到
;依此規(guī)律得到 級分形圖.
級分形圖.
(1) 級分形圖中共有 條線段;
級分形圖中共有 條線段;
(2) 級分形圖中所有線段長度之和為 .
級分形圖中所有線段長度之和為 .
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
已知數(shù)列{an}的前n項(xiàng)和為Sn,a1=2.當(dāng)n≥2時,Sn-1+1,an,Sn+1成等差數(shù)列.
(1)求證:{Sn+1}是等比數(shù)列;
(2)求數(shù)列{nan}的前n項(xiàng)和Tn.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
已知 是各項(xiàng)均為正數(shù)的等比數(shù)列,且
是各項(xiàng)均為正數(shù)的等比數(shù)列,且 ,
,
(1)求 的通項(xiàng)公式;
的通項(xiàng)公式;
(2)設(shè) 求數(shù)列
求數(shù)列 的前
的前 項(xiàng)和
項(xiàng)和 .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
已知數(shù)列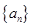 和
和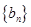 滿足:
滿足: ,其中
,其中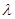 為實(shí)數(shù),
為實(shí)數(shù),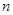 為正整數(shù).
為正整數(shù).
(1)對任意實(shí)數(shù)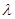 ,求證:
,求證: 不成等比數(shù)列;
不成等比數(shù)列;
(2)試判斷數(shù)列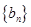 是否為等比數(shù)列,并證明你的結(jié)論.
是否為等比數(shù)列,并證明你的結(jié)論.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
某市為控制大氣PM2.5的濃度,環(huán)境部門規(guī)定:該市每年的大氣主要污染物排放總量不能超過55萬噸,否則將采取緊急限排措施.已知該市2013年的大氣主要污染物排放總量為40萬噸,通過技術(shù)改造和倡導(dǎo)綠色低碳生活等措施,此后每年的原大氣主要污染物排放最比上一年的排放總量減少10%.同時,因?yàn)榻?jīng)濟(jì)發(fā)展和人口增加等因素,每年又新增加大氣主要污染物排放量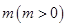 萬噸.
萬噸.
(1)從2014年起,該市每年大氣主要污染物排放總量(萬噸)依次構(gòu)成數(shù)列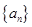 ,求相鄰兩年主要污染物排放總量的關(guān)系式;
,求相鄰兩年主要污染物排放總量的關(guān)系式;
(2)證明:數(shù)列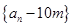 是等比數(shù)列;
是等比數(shù)列;
(3)若該市始終不需要采取緊急限排措施,求m的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
我們把一系列向量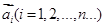 排成一列,稱為向量列,記作
排成一列,稱為向量列,記作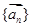 ,又設(shè)
,又設(shè)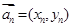 ,假設(shè)向量列
,假設(shè)向量列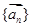 滿足:
滿足: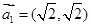 ,
,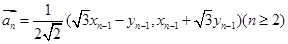 。
。
(1)證明數(shù)列 是等比數(shù)列;
是等比數(shù)列;
(2)設(shè)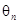 表示向量
表示向量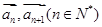 間的夾角,若
間的夾角,若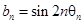 ,記
,記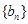 的前
的前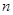 項(xiàng)和為
項(xiàng)和為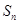 ,求
,求 ;
;
(3)設(shè)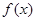 是
是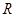 上不恒為零的函數(shù),且對任意的
上不恒為零的函數(shù),且對任意的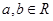 ,都有
,都有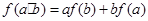 ,若
,若 ,
,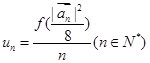 ,求數(shù)列
,求數(shù)列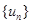 的前
的前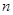 項(xiàng)和
項(xiàng)和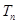 .
.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com