中文字幕人妻色偷偷久久-精品久久久久成人码免费动漫-久久精品国产清自在天天线-国产成人精品免高潮在线观看

精英家教網 > 高中數學 > 題目詳情
若函數數f(x)=
1
2
x2-
a
b
x-
1
b
在x=0處的切線l與圓C：x2+y2=1相離，則P（a，b）與圓C的位置關系是（　　）
分析：利用導數求出函數f(x)=
1
2
x2-
a
b
x-
1
b
在x=0處的切線l的方程，由l與圓C：x2+y2=1相離得到圓心（0，0）到直線l的距離大于圓的半徑，整理后得到
a2+b2
＜1．從而得到答案．
解答：解：由f(x)=
1
2
x2-
a
b
x-
1
b
，得f′(x)=x-
a
b
，
∴f′（0）=-
a
b
，又f（0）=-
1
b
．
∴函數f(x)=
1
2
x2-
a
b
x-
1
b
在x=0處的切線l為：y+
1
b
=-
a
b
(x-0)，即ax+by+1=0．
∵l與圓C：x2+y2=1相離，
∴圓心（0，0）到直線l的距離大于圓的半徑1．
即
1
a2+b2
＞1，
a2+b2
＜1．
∴P（a，b）在圓x2+y2=1的內部．
故選：A．
點評：本題考查了利用導數研究曲線上某點處的切線方程，考查了直線與圓的位置關系，考查了點到直線的距離公式，是中檔題．
練習冊系列答案
相關習題

科目：高中數學 來源： 題型：

解：因為有負根，所以在y軸左側有交點，因此

解：因為函數沒有零點，所以方程無根，則函數y=x+|x-c|與y=2沒有交點，由圖可知c>2


 13．證明：（1）令x=y=1,由已知可得f(1)=f(1×1)=f(1)f(1),所以f(1)=1或f(1)=0

若f(1)=0，f(0)=f(1×0)=f(1)f(0)=0，所以f(1)=f(0)與已知條件“”矛盾所以f(1)≠0，因此f(1)=1,所以f(1)-1=0，1是函數y=f(x)-1的零點

（2）因為f(1)=f[(-1)×（-1）]=f2(-1)=,所以f(-1)=±1，但若f(-1)=1,則f(-1)=f(1)與已知矛盾所以f(-1)不能等于1，只能等于-1。所以任x∈R，f(-x)=f(-1)f(x)=-f(x)，因此函數是奇函數

數字1，2，3，4恰好排成一排，如果數字i（i=1，2，3，4）恰好出現在第i個位置上則稱有一個巧合，求巧合數的分布列。

查看答案和解析>>

科目：高中數學 來源：0117 模擬題 題型：解答題

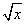由函數y=f(x)確定數列{an}，an=f(n)，若函數y=f(x)的反函數y=f-1(x)能確定數列{bn}，bn=f-1(n)，則稱數列{bn}是數列{an}的“反數列”。
（1）若函數f(x)=2確定數列{an}的反數列為{bn}，求{bn}的通項公式；
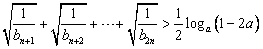（2）對（1）中{bn}，不等式對任意的正整數n恒成立，求實數a的取值范圍；
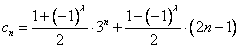（3）設（λ為正整數），若數列{cn}的反數列為{dn}，{cn}與{dn}的公共項組成的數列為{tn}， 求數列{tn}前n項和Sn。

查看答案和解析>>

科目：高中數學 來源： 題型：

下面是三位同學的說法,請判斷正誤:

甲生:有窮數列1,3,5,7,…,2n－3的項數為n；

乙生:數列{－0.3n2+2n+7}中的最大項的值為；

丙生:若函數y=f(x)不單調,則數列{f(n)}也不單調.

查看答案和解析>>

科目：高中數學 來源： 題型：

由函數y=f(x)確定數列{an},an=f(n),若函數y=f(x)的反函數y=f-1(x)能確定數列{bn},bn=f-1(n),則稱數列{bn}是數列{an}的“反數列”.

(1)已知函數f(x)=2的反函數為f-1(x)=(x≥0),則由函數f(x)=2確定的數列{an}的反數列為{bn},求{bn}的通項公式;不等式++…+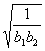≥1-2a對任意的正整數n恒成立,求實數a的范圍;

(2)設函數y=3x確定的數列為{cn},{cn}的反數列為{dn},{cn}與{dn}的公共項組成的數列為{tn},求數列{tn}的前n項和Sn.

查看答案和解析>>

同步練習冊答案