
已知函數![]() 其中
其中![]()
(1)證明函數f(x)的圖像在y軸的一側;
(2)求函數![]() 與
與![]() 的圖像的公共點的坐標。
的圖像的公共點的坐標。
 口算心算速算應用題系列答案
口算心算速算應用題系列答案 同步拓展閱讀系列答案
同步拓展閱讀系列答案科目:高中數學 來源:2013-2014學年福建省福州市高三畢業班質檢文科數學試卷(解析版) 題型:解答題
已知函數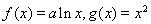 .其中
.其中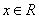 .
.
(1)若曲線y=f(x)與y=g(x)在x=1處的切線相互平行,求兩平行直線間的距離;
(2)若f(x)≤g(x)-1對任意x>0恒成立,求實數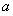 的值;
的值;
(3)當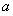 <0時,對于函數h(x)=f(x)-g(x)+1,記在h(x)圖象上任取兩點A、B連線的斜率為
<0時,對于函數h(x)=f(x)-g(x)+1,記在h(x)圖象上任取兩點A、B連線的斜率為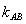 ,若
,若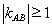 ,求
,求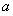 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源:2013-2014學年江蘇鹽城第一中學高三第二學期期初檢測文科數學試卷(解析版) 題型:解答題
已知函數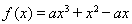 ,其中
,其中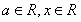 .
.
(1)當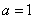 時,求函數
時,求函數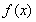 在
在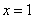 處的切線方程;
處的切線方程;
(2)若函數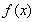 在區間(1,2)上不是單調函數,試求
在區間(1,2)上不是單調函數,試求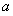 的取值范圍;
的取值范圍;
(3)已知 ,如果存在
,如果存在 ,使得函數
,使得函數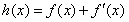
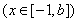 在
在 處取得最小值,試求
處取得最小值,試求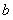 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源:2013屆浙江寧波四校高二下學期期中聯考理科數學試卷(解析版) 題型:解答題
已知函數 , 其中
, 其中 .
.
(1)當 時,求曲線
時,求曲線 在點
在點 處的切線方程;
處的切線方程;
(2)當 時,求曲線
時,求曲線 的單調區間與極值.
的單調區間與極值.
【解析】第一問中利用當 時,
時, ,
,
 ,得到切線方程
,得到切線方程
第二問中,

對a分情況討論,確定單調性和極值問題。
解: (1) 當 時,
時, ,
,
 ………………………….2分
………………………….2分

 切線方程為:
切線方程為:  …………………………..5分
…………………………..5分
(2) 
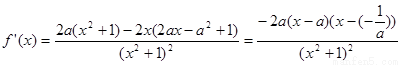 …….7
…….7 分
分
分類: 當 時, 很顯然
時, 很顯然
 的單調增區間為:
的單調增區間為:  單調減區間:
單調減區間:  ,
,
 ,
,  ………… 11分
………… 11分
當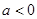 時
時 的單調減區間:
的單調減區間:  單調增區間:
單調增區間: 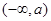 ,
,

 ,
, 
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com