已知數(shù)列
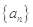
的前
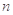
項和為
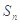
,且滿足
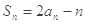
,
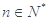
(1)求數(shù)列
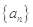
的通項公式;
(2)求證:
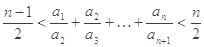
(1)
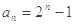
;(2)
試題分析:(1)根據(jù)題中已知條件
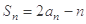
,得出
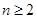
時,
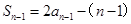
此兩式作差整理即可得到形如的數(shù)列
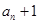
所滿足的關系,從而可求出數(shù)列
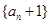
的通項公式得到所求;
(2)
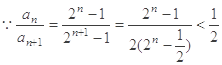
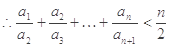
,
又
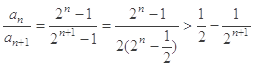
,利用放縮法即可得證.
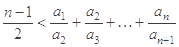
(1)因為
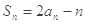
,………①
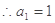
,且
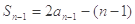
……… ②
①-②得

,
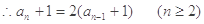
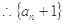
是首項為2,公比為2的等比數(shù)列,
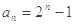
(2)證明:
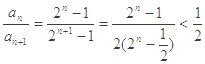
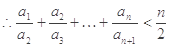
.
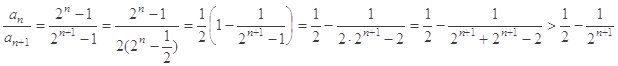
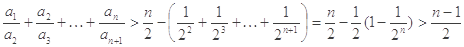
∴
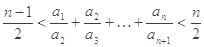
.
練習冊系列答案
相關習題
科目:高中數(shù)學
來源:不詳
題型:解答題
若數(shù)列
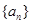
滿足條件:存在正整數(shù)
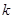
,使得
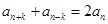
對一切
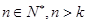
都成立,則稱數(shù)列
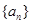
為
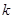
級等差數(shù)列.
(1)已知數(shù)列
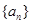
為2級等差數(shù)列,且前四項分別為
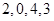
,求
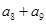
的值;
(2)若
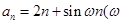
為常數(shù)),且
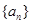
是
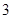
級等差數(shù)列,求
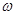
所有可能值的集合,并求
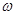
取最小正值時數(shù)列
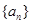
的前3
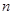
項和
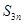
;
(3)若
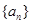
既是
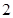
級等差數(shù)列
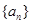
,也是
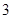
級等差數(shù)列,證明:
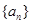
是等差數(shù)列.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
已知數(shù)列
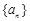
的首項
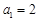
,且
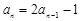
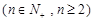
.
(1)求數(shù)列
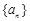
的通項公式;
(2)求數(shù)列
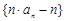
的前
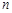
項和
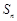
.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
已知
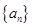
是各項均為正數(shù)的等比數(shù)列,且
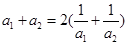
,
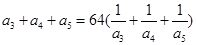
(1)求
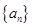
的通項公式;
(2)設
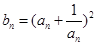
求數(shù)列
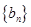
的前
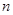
項和
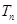
.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
[2013·廣東高考]設數(shù)列{an}是首項為1,公比為-2的等比數(shù)列,則a1+|a2|+a3+|a4|=________.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
設數(shù)列
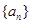
滿足

,
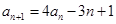
,
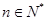
,則數(shù)列
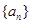
的前n項和為
.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
(2011•山東)等比數(shù)列{a
n}中,a
1,a
2,a
3分別是下表第一、二、三行中的某一個數(shù),且其中的任何兩個數(shù)不在下表的同一列.
| 第一列
| 第二列
| 第三列
|
第一行
| 3
| 2
| 10
|
第二行
| 6
| 4
| 14
|
第三行
| 9
| 8
| 18
|
(1)求數(shù)列{a
n}的通項公式;
(2)若數(shù)列{b
n}滿足:b
n=a
n+(﹣1)
nlna
n,求數(shù)列{b
n}的前2n項和S
2n.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
設數(shù)列
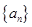
滿足
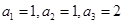
,若
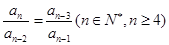
,則
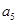
=
,
數(shù)列
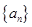
的前10項和
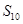
=
.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
在等比數(shù)列
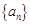
中,若
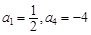
,則
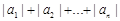
=____________.
查看答案和解析>>

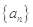 的前
的前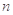 項和為
項和為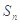 ,且滿足
,且滿足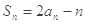 ,
,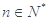
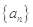 的通項公式;
的通項公式;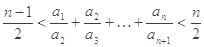
 閱讀快車系列答案
閱讀快車系列答案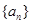 滿足條件:存在正整數(shù)
滿足條件:存在正整數(shù)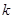 ,使得
,使得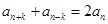 對一切
對一切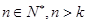 都成立,則稱數(shù)列
都成立,則稱數(shù)列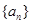 為
為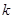 級等差數(shù)列.
級等差數(shù)列.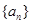 為2級等差數(shù)列,且前四項分別為
為2級等差數(shù)列,且前四項分別為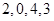 ,求
,求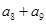 的值;
的值;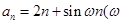 為常數(shù)),且
為常數(shù)),且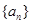 是
是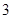 級等差數(shù)列,求
級等差數(shù)列,求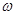 所有可能值的集合,并求
所有可能值的集合,并求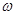 取最小正值時數(shù)列
取最小正值時數(shù)列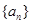 的前3
的前3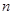 項和
項和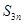 ;
;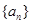 既是
既是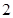 級等差數(shù)列
級等差數(shù)列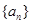 ,也是
,也是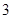 級等差數(shù)列,證明:
級等差數(shù)列,證明: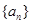 是等差數(shù)列.
是等差數(shù)列.