
已知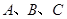 為銳角
為銳角 的三個內角,向量
的三個內角,向量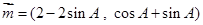 與
與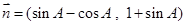 共線.
共線.
(1)求角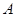 的大小;
的大小;
(2)求角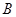 的取值范圍
的取值范圍
(3)求函數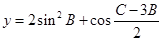 的值域.
的值域.
(1)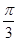 ;(2)
;(2)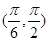 ;(3)(
;(3)(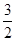 ,2]
,2]
解析試題分析:(1)由向量平行的坐標形式及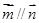 可列出關于角A的正弦的方程,求出
可列出關于角A的正弦的方程,求出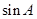 ,結合A為銳角,求出A角;(2)由(1)知A的值,從而求出B+C的值,將C用B表示出來,結合B、C都是銳角,列出關于B的不等式組,從而求出B的范圍;(3)將函數式中C用B表示出來,化為B的函數,用降冪公式及輔助角公式化為一個角的三角函數,按照復合函數求值域的方法,結合(2)中B角的范圍,求出內函數的值域,作為中間函數的定義域,利用三角函數圖像求出中間函數的值域,作為外函數的定義域,再利用外函數的性質求出外函數的值域即為所求函數的值域.
,結合A為銳角,求出A角;(2)由(1)知A的值,從而求出B+C的值,將C用B表示出來,結合B、C都是銳角,列出關于B的不等式組,從而求出B的范圍;(3)將函數式中C用B表示出來,化為B的函數,用降冪公式及輔助角公式化為一個角的三角函數,按照復合函數求值域的方法,結合(2)中B角的范圍,求出內函數的值域,作為中間函數的定義域,利用三角函數圖像求出中間函數的值域,作為外函數的定義域,再利用外函數的性質求出外函數的值域即為所求函數的值域.
試題解析:(1)由題設知: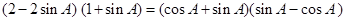
得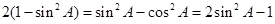 即
即 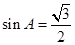
由△ABC是銳角三角形知: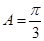 4分
4分
(2)由(1)及題設知: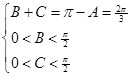 即
即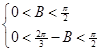 得
得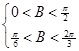
∴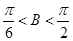 8分
8分
(3)由(1)及題設知: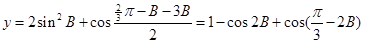
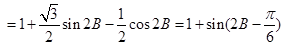 , 10分
, 10分
由(2)知: 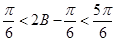
∴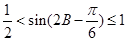 12分
12分
∴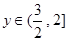
因此函數y=2sin2B+cos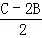 的值域為(
的值域為(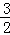 ,2] 14分
,2] 14分
(其他寫法參照給分)
考點:向量平行的充要條件;已知函數值求角;不等式性質;三角變換;三角函數在某個區間上的值域


湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com