Question

設橢圓+y²=1的兩個焦點是F₁（-c,0）與F₂（c,0）(c＞0),且橢圓上存在點M，使得·=0.

（1）求實數(shù)m的取值范圍；

（2）在直線l:y=x+2上存在一點E，使得?|EF₁|+|EF₂|取得最小值，求此最小值及此時橢圓的方程；

（3）在條件（2）下的橢圓方程，是否存在斜率為k（k≠0）的直線l與橢圓交于不同的兩點A、B，滿足=，且使得過點N（0，-1）、Q的直線，有·=0？若存在，求出k的取值范圍，若不存在，說明理由.

Answer 1

解析：（1）∵|MF₁|+|MF₂|=2,|MF₁|²+|MF₂|²=4m,

而|MF₁|²+|MF₂|²≥，

∴4m≥2(m+1),解得m≥1.

（2）由

得(m+2)x²+4(m+1)x+3(m+1)=0.

Δ=16(m+1)²-12(m+2)(m+1)=4(m+1)(m-2)≥0.

解得m≥2或m≤-1（舍去），∴m≥2.

此時|EF₁|+|EF₂|=2m+1≥2,

當且僅當m=2時|EF₁|+|EF₂|取得最小值2，此時橢圓方程為+y²=1.

（3）設兩點AB的坐標分別為A（x₁,y₁）、B（x₂,y₂），中點Q（x,y），

則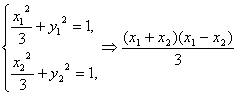+(y₁+y₂)(y₁-y₂)=0,

∴AB中點Q的軌跡為直線

y=-x                                                                                                          ①

在橢圓內的部分.

又由·=0，得過點N（0，-1），且斜率為-的直線方程為y=-x-1,          ②

由①②可得點Q的坐標為（,）,

∵點Q必在橢圓內，

∴＜1.解得k²＜1,

又k≠0,∴k∈(-1,0)∪(0,1).