
中國航母“遼寧艦”是中國第一艘航母,“遼寧”號以4臺蒸汽輪機為動力,為保證航母的動力安全性,科學家對蒸汽輪機進行了170余項技術改進,增加了某項新技術,該項新技術要進入試用階段前必須對其中的三項不同指標甲、乙、丙進行通過量化檢測.假如該項新技術的指標甲、乙、丙獨立通過檢測合格的概率分別為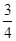 、
、 、
、 .指標甲、乙、丙合格分別記為4分、2分、4分;若某項指標不合格,則該項指標記0分,各項指標檢測結果互不影響.
.指標甲、乙、丙合格分別記為4分、2分、4分;若某項指標不合格,則該項指標記0分,各項指標檢測結果互不影響.
(I)求該項技術量化得分不低于8分的概率;
(II)記該項新技術的三個指標中被檢測合格的指標個數為隨機變量X,求X的分布列與數學期望.
(1)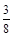
(2))隨機變量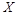 的分布列為
的分布列為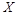
0 1 2 3 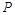
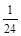
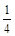
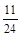
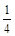
 =
=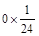 +
+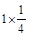 +
+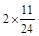 +
+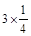 =
=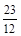
解析試題分析:.解:(Ⅰ)該項新技術的三項不同指標甲、乙、丙獨立通過檢測合格分別為事件
科目:高中數學
來源:
題型:解答題
下圖是某市3月1日至14日的空氣質量指數趨勢圖,空氣質量指數小于100表示空氣質量優良,空氣質量指數大于200表示空氣重度污染,某人隨機選擇3月1日至3月13日中的某一天到達該市,并停留2天
科目:高中數學
來源:
題型:解答題
某超市為了解顧客的購物量及結算時間等信息,安排一名員工隨機收集了在該超市購物的100位顧客的相關數據,如下表所示.
科目:高中數學
來源:
題型:解答題
一個路口的紅綠燈,紅燈的時間為30秒,黃燈的時間為5秒,綠燈的時間為
科目:高中數學
來源:
題型:解答題
某學校籃球隊、羽毛球隊、乒乓球隊的某些隊員不止參加了一支球隊,具體情況如圖所示,現從中隨機抽取一名隊員,求:
科目:高中數學
來源:
題型:解答題
甲與乙兩人擲硬幣,甲用一枚硬幣擲3次,記正面朝上的次數為
科目:高中數學
來源:
題型:解答題
“中國式過馬路”存在很大的交通安全隱患.某調
科目:高中數學
來源:
題型:解答題
某高校在2011年的自主招生考試成績中隨機抽取 100名學生的筆試成績,按成績分組,得到的頻率分布表如下所示.
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區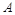 、
、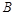 、
、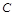 ,
,
則事件“得分不低于8分”表示為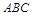 +
+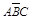 .
. 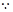
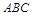 與
與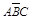 為互斥事件,且
為互斥事件,且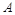 、
、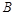 、
、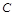 為彼此獨立
為彼此獨立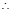
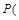
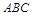 +
+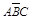
 =
=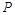 (
(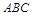 )+
)+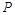 (
(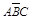 ) =
) =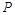 (
(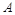 )
)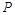 (
(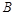 )
)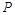 (
(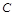 )+
)+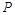 (
(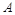 )
)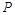 (
(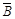 )
)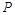 (
(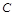 =
=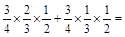
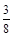 . 4分
. 4分
(Ⅱ)該項新技術的三個指標中被檢測合格的指標個數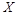 的取值為0,1,2,3.
的取值為0,1,2,3.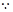
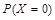 =
=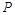 (
(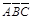 )=
)=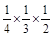 =
=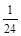 ,
,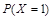 =
=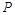 (
(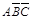 +
+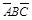 +
+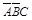 )=
)=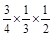 +
+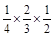 +
+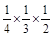 =
=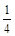 ,
,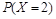 =
=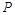 (
(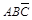 +
+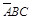 +
+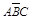 )=
)=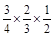 +
+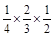 +
+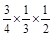 =
=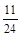 ,
,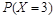 =
=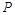 (
(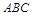 )=
)=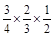 =
=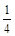 , 8分
, 8分
隨機變量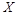 的分布列為
的分布列為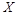
0 1 2


西城學科專項測試系列答案
小考必做系列答案
小考實戰系列答案
小考復習精要系列答案
小考總動員系列答案
小升初必備沖刺48天系列答案
68所名校圖書小升初高分奪冠真卷系列答案
伴你成長周周練月月測系列答案
小升初金卷導練系列答案
萌齊小升初強化模擬訓練系列答案
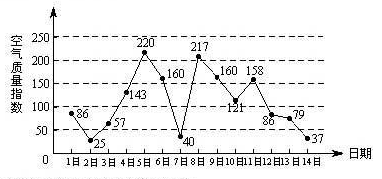
(Ⅰ)求此人到達當日空氣重度污染的概率
(Ⅱ)設X是此人停留期間空氣質量優良的天數,求X的分布列與數學期望.
(Ⅲ)由圖判斷從哪天開始連續三天的空氣質量指數方差最大?(結論不要求證明)
已知這100位顧客中的一次購物量超過8件的顧客占55%.一次購物量
1至4件
5至8件
9至12件
13至16件
17件及以上
顧客數(人)

30
25

10
結算時間(分鐘/人)
1
1.5
2
2.5
3
(Ⅰ)確定x,y的值,并求顧客一次購物的結算時間X的分布列與數學期望;
(Ⅱ)若某顧客到達收銀臺時前面恰有2位顧客需結算,且各顧客的結算相互獨立,求該顧客結算前的等候時間不超過2.5分鐘的概率.(注:將頻率視為概率)
40秒,當你到達路口時看見下列三種情況的概率各是多少?
(1) 紅燈 (2) 黃燈 (3) 不是紅燈
(1)該隊員只屬于一支球隊的概率;
(2)該隊員最多屬于兩支球隊的概率.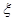 ;乙用這枚硬幣擲2次,記正面朝上的次數為
;乙用這枚硬幣擲2次,記正面朝上的次數為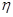 。
。
(1)分別求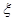 與
與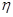 的期望;
的期望;
(2)規定:若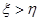 ,則甲獲勝;若
,則甲獲勝;若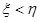 ,則乙獲勝,分別求出甲和乙獲勝的概率.
,則乙獲勝,分別求出甲和乙獲勝的概率.
查機構為了解路人對“中國式過馬路”的態度是否與性別有關,從馬路旁隨機抽取30名路
人進行了問卷調查,得到了如下列聯表:
已知在這30人中隨機抽取1人抽到反感“中國式過馬路”的路人的概率是 男性 女性 合計 反感 10 不反感 8 合計 30  .
.
(Ⅰ)請將上面的列聯表補充完整(在答題卡上直接填寫結果,不需要寫求解過程),并據此資料分析反感“中國式過馬路”與性別是否有關?
(Ⅱ)若從這30人中的女性路人中隨機抽取2人參加一活動,記反感“中國式過馬路”的人數為X,求X的分布列和數學期望.
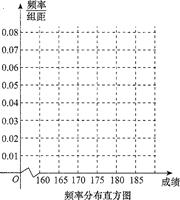
(1)請先求出頻率分布表中①,②位置相應的數據,再完成下列頻率分布直方圖;并確定中位數。(結果保留2位小數)
(2)為了能選拔出最優秀的學生,高校決定在筆試成績高的第3,4,5組中用分層抽樣抽取6名學生進入第二輪面試,求第3,4,5組每組各抽取多少名學生進入第二輪面試?
(3)在(2)的條件下,學校決定在6名學生中隨機抽取2名學生接受考官進行面試,求第4組至少有一名學生被考官A面試的概率?
版權聲明:本站所有文章,圖片來源于網絡,著作權及版權歸原作者所有,轉載無意侵犯版權,如有侵權,請作者速來函告知,我們將盡快處理,聯系qq:3310059649。
ICP備案序號: 滬ICP備07509807號-10 鄂公網安備42018502000812號