
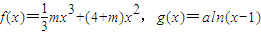 ,其中a≠0.
,其中a≠0.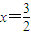 的對稱點在y=f(x)的圖象上,求m的值;
的對稱點在y=f(x)的圖象上,求m的值;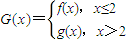 ,曲線y=G(x)上是否存在兩點P、Q,使△OPQ(O為原點)是以O為直角頂點的直角三角形,且斜邊的中點在y軸上?如果存在,求a的取值范圍;如果不存在,說明理由.
,曲線y=G(x)上是否存在兩點P、Q,使△OPQ(O為原點)是以O為直角頂點的直角三角形,且斜邊的中點在y軸上?如果存在,求a的取值范圍;如果不存在,說明理由.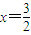 的對稱點(1,0),由題意可得f(1)=0,求出m的值;
的對稱點(1,0),由題意可得f(1)=0,求出m的值;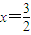 的對稱點(1,0),
的對稱點(1,0), m+4+m=0,m=-3.
m+4+m=0,m=-3.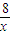 =
=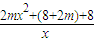 =
=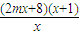 ,
, ,由F′(x)<0得x>-
,由F′(x)<0得x>-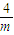 ,
,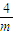 )上是增函數,在(-
)上是增函數,在(-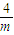 ,+∞)上是減函數,
,+∞)上是減函數,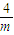 ,由F′(x)<0得x>-
,由F′(x)<0得x>-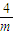 ,此時,F(x)在(0,-
,此時,F(x)在(0,-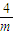 )上是增函數,在(-
)上是增函數,在(-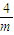 ,+∞)上是減函數,
,+∞)上是減函數, ,
,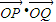 =0,即-t2+G(t)(t3+t2)=0,①
=0,即-t2+G(t)(t3+t2)=0,①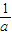 =(t+1)ln(t-1),設h(x)=(t+1)ln(t-1),則h′(x)=ln(t-1)+
=(t+1)ln(t-1),設h(x)=(t+1)ln(t-1),則h′(x)=ln(t-1)+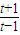 ,
,

科目:高中數學 來源: 題型:
| π |
| 6 |
| π |
| 2 |
查看答案和解析>>
科目:高中數學 來源:2011-2012學年湖北省鄂州二中高三(上)10月段考數學試卷(解析版) 題型:解答題
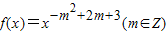 為偶函數,且在區間(0,+∞)上是單調增函數
為偶函數,且在區間(0,+∞)上是單調增函數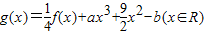 ,其中a,b∈R.若函數g(x)僅在x=0處有極值,求a的取值范圍.
,其中a,b∈R.若函數g(x)僅在x=0處有極值,求a的取值范圍.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
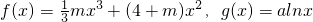 ,其中a≠0.
,其中a≠0.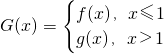 ,曲線y=G(x)上是否存在兩點P、Q,使△OPQ(O為原點)是以O為直角頂點的直角三角形,且該三角形斜邊的中點在y軸上?如果存在,求a的取值范圍;如果不存在,說明理由.
,曲線y=G(x)上是否存在兩點P、Q,使△OPQ(O為原點)是以O為直角頂點的直角三角形,且該三角形斜邊的中點在y軸上?如果存在,求a的取值范圍;如果不存在,說明理由.查看答案和解析>>
科目:高中數學 來源:2013年山東省濰坊市高考數學一模試卷(文科)(解析版) 題型:解答題
 ,其中a≠0.
,其中a≠0.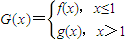 ,曲線y=G(x)上是否存在兩點P、Q,使△OPQ(O為原點)是以O為直角頂點的直角三角形,且該三角形斜邊的中點在y軸上?如果存在,求a的取值范圍;如果不存在,說明理由.
,曲線y=G(x)上是否存在兩點P、Q,使△OPQ(O為原點)是以O為直角頂點的直角三角形,且該三角形斜邊的中點在y軸上?如果存在,求a的取值范圍;如果不存在,說明理由.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com