
設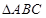 的三個內角分別為
的三個內角分別為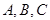 .向量
.向量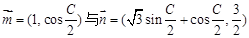 共線.
共線.
(Ⅰ)求角 的大小;
的大小;
(Ⅱ)設角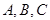 的對邊分別是
的對邊分別是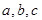 ,且滿足
,且滿足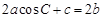 ,試判斷
,試判斷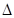
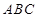 的形狀.
的形狀.
(Ⅰ)C=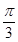 ;(Ⅱ)△
;(Ⅱ)△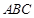 為等邊三角形
為等邊三角形
解析試題分析:(Ⅰ)∵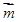 與
與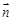 共線,∴
共線,∴ 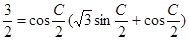
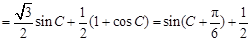 3分
3分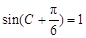 ∴C=
∴C=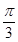 6分
6分
(Ⅱ)由已知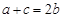 根據余弦定理可得:
根據余弦定理可得: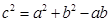 8分
8分
聯立解得: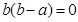

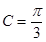 ,所以△
,所以△ 為等邊三角形, 12分
為等邊三角形, 12分
考點:本題考查了數量積的坐標運算及三角函數的恒等變換、余弦定理
點評:三角形的形狀的判定常常通過正弦定理和余弦定理,將已知條件中的邊角關系轉化為純邊或純角的關系,尋找邊之間的關系或角之間關系來判定.一般的,利用正弦定理的公式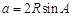 ,
,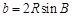 ,
,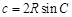 ,可將邊轉化為角的三角函數關系,然后利用三角函數恒等式進行化簡,其中往往用到三角形內角和定理:
,可將邊轉化為角的三角函數關系,然后利用三角函數恒等式進行化簡,其中往往用到三角形內角和定理: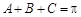 ;利用余弦定理公式
;利用余弦定理公式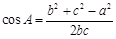 ,
, ,
,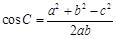 ,可將有關三角形中的角的余弦轉化為邊的關系,然后充分利用代數知識來解決問題.
,可將有關三角形中的角的余弦轉化為邊的關系,然后充分利用代數知識來解決問題.


 期末好成績系列答案
期末好成績系列答案 99加1領先期末特訓卷系列答案
99加1領先期末特訓卷系列答案 百強名校期末沖刺100分系列答案
百強名校期末沖刺100分系列答案科目:高中數學 來源: 題型:解答題
如圖,在直角坐標系 中,角
中,角 的頂點是原點,始邊與
的頂點是原點,始邊與 軸正半軸重合,終邊交單位圓于點
軸正半軸重合,終邊交單位圓于點 ,且
,且 .將角
.將角 的終邊按逆時針方向旋轉
的終邊按逆時針方向旋轉 ,交單位圓于點
,交單位圓于點 .記
.記 .
.
(Ⅰ)若 ,求
,求 ;
;
(Ⅱ)分別過 作
作 軸的垂線,垂足依次為
軸的垂線,垂足依次為 .記△
.記△ 的面積為
的面積為 ,△
,△ 的面積為
的面積為 .若
.若 ,求角
,求角 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com