
已知函數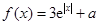 (
(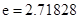 是自然對數的底數)的最小值為
是自然對數的底數)的最小值為 .
.
(Ⅰ)求實數 的值;
的值;
(Ⅱ)已知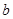
 且
且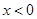 ,試解關于
,試解關于 的不等式
的不等式 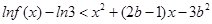 ;
;
(Ⅲ)已知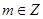 且
且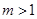 .若存在實數
.若存在實數 ,使得對任意的
,使得對任意的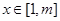 ,都有
,都有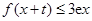 ,試求
,試求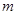 的最大值.
的最大值.
(1)
(2)當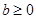 時,不等式的解為
時,不等式的解為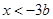 ;當
;當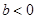 時,不等式的解為
時,不等式的解為
(3)3
解析試題分析:解:(Ⅰ)因為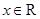 ,所以
,所以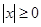 ,故
,故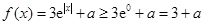 ,
,
因為函數 的最小值為
的最小值為 ,所以
,所以 . 3分
. 3分
(Ⅱ)由(Ⅰ)得,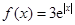 .
.
當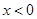 時,
時,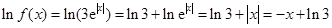 , 5分
, 5分
故不等式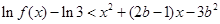 可化為:
可化為: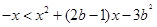 ,
,
即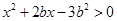 , 6分
, 6分
得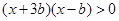 ,
,
所以,當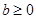 時,不等式的解為
時,不等式的解為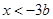 ;
;
當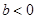 時,不等式的解為
時,不等式的解為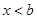 . 8分
. 8分
(Ⅲ)∵當 且
且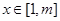 時,
時,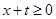 ,
,
∴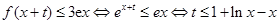 .
.
∴原命題等價轉化為:存在實數 ,使得不等式
,使得不等式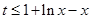 對任意
對任意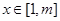 恒成立. 10分
恒成立. 10分
令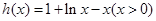 .
.
∵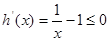 ,∴函數
,∴函數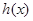 在
在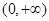 為減函數. 11分
為減函數. 11分
又∵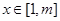 ,∴
,∴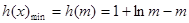 . 12分
. 12分
∴要使得對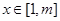 ,
,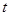 值恒存在,只須
值恒存在,只須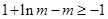 . 13分
. 13分
∵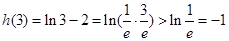 ,
,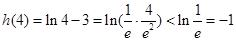
且函數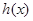 在
在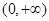 為減函數,
為減函數,
∴滿足條件的最大整數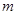 的值為3. 14分
的值為3. 14分
考點:函數與不等式
點評:主要是考查了函數與不等式的綜合運用,以及導數研究函數單調性的求解屬于中檔題。


科目:高中數學 來源: 題型:解答題
已知一家公司生產某種產品的年固定成本為10萬元,每生產1千件該產品需另投入2.7萬元,設該公司一年內生產該產品 千件并全部銷售完,每千件的銷售收入為
千件并全部銷售完,每千件的銷售收入為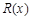 萬元,且
萬元,且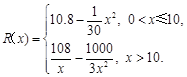
(Ⅰ)寫出年利潤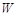 (萬元)關于年產量
(萬元)關于年產量 (千件)的函數解析式;
(千件)的函數解析式;
(Ⅱ)年產量為多少千件時,該公司在這一產品的產銷過程中所獲利潤最大
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某單位設計的兩種密封玻璃窗如圖所示:圖1是單層玻璃,厚度為8 mm;圖2是雙層中空玻璃,厚度均為4 mm,中間留有厚度為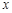 的空氣隔層.根據熱傳導知識,對于厚度為
的空氣隔層.根據熱傳導知識,對于厚度為 的均勻介質,兩側的溫度差為
的均勻介質,兩側的溫度差為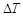 ,單位時間內,在單位面積上通過的熱量
,單位時間內,在單位面積上通過的熱量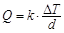 ,其中
,其中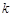 為熱傳導系數.假定單位時間內,在單位面積上通過每一層玻璃及空氣隔層的熱量相等.(注:玻璃的熱傳導系數為
為熱傳導系數.假定單位時間內,在單位面積上通過每一層玻璃及空氣隔層的熱量相等.(注:玻璃的熱傳導系數為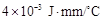 ,空氣的熱傳導系數為
,空氣的熱傳導系數為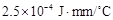 .)
.)
(1)設室內,室外溫度均分別為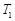 ,
,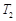 ,內層玻璃外側溫度為
,內層玻璃外側溫度為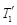 ,外層玻璃內側溫度為
,外層玻璃內側溫度為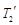 ,且
,且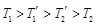 .試分別求出單層玻璃和雙層中空玻璃單位時間內,在單位面積上通過的熱量(結果用
.試分別求出單層玻璃和雙層中空玻璃單位時間內,在單位面積上通過的熱量(結果用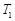 ,
,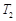 及
及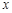 表示);
表示);
(2)為使雙層中空玻璃單位時間內,在單位面積上通過的熱量只有單層玻璃的4%,應如何設計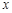 的大小?
的大小?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
甲廠以x 千克/小時的速度運輸生產某種產品(生產條件要求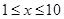 ),每小時可獲得利潤是
),每小時可獲得利潤是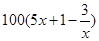 元.
元.
(1)要使生產該產品2小時獲得的利潤不低于3000元,求x的取值范圍;
(2)要使生產900千克該產品獲得的利潤最大,問:甲廠應該選取何種生產速度?并求最大利潤.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(1)已知函數y=ln(-x2+x-a)的定義域為(-2,3),求實數a的取值范圍;
(2)已知函數y=ln(-x2+x-a)在(-2,3)上有意義,求實數a的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com