
已知函數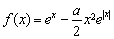 .
.
(Ⅰ)若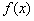 是
是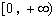 上是增函數,求實數a的取值范圍;
上是增函數,求實數a的取值范圍;
(Ⅱ)證明:當a≥1時,證明不等式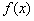 ≤x+1對x∈R恒成立;
≤x+1對x∈R恒成立;
(Ⅲ)對于在(0,1)中的任一個常數a,試探究是否存在x0>0,使得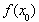 >x0+1成立?如果存在,請求出符合條件的一個x0;如果不存在,請說明理由.
>x0+1成立?如果存在,請求出符合條件的一個x0;如果不存在,請說明理由.
(I)a的取值范圍為a≤0;(Ⅱ)詳見解析;(Ⅲ)可找到一個常數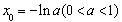 ,使得
,使得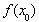 >x0+1成立.
>x0+1成立.
【解析】
試題分析:(I)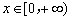 時,
時,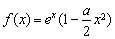 ,求導得
,求導得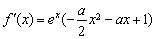 .由題意,
.由題意,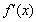 ≥0在
≥0在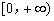 上恒成立.因為ex>0恒成立,故只需
上恒成立.因為ex>0恒成立,故只需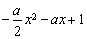 ≥0在
≥0在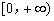 上恒成立,結合拋物線的圖象即可得a的取值范圍;(Ⅱ)由題知f(x)≤x+1即為
上恒成立,結合拋物線的圖象即可得a的取值范圍;(Ⅱ)由題知f(x)≤x+1即為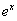 -
-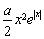 ≤x+1.由于含有
≤x+1.由于含有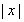 ,故分
,故分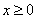 和
和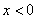 兩種情況討論.①在x≥0時,要證明
兩種情況討論.①在x≥0時,要證明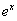 -
-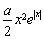 ≤x+1成立,可變為證1≤
≤x+1成立,可變為證1≤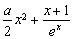 成立,這樣只需利用導數求
成立,這樣只需利用導數求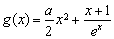 的最小值即可,求導得
的最小值即可,求導得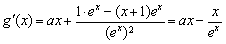 ,易得
,易得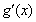 ≥0,從而g(x)≥g(0)=1.注:直接證
≥0,從而g(x)≥g(0)=1.注:直接證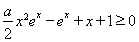 也可,只是需要求兩次導數.
也可,只是需要求兩次導數.
②在x≤0時,要證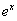 -
-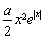 ≤x+1成立,可變為證1≤
≤x+1成立,可變為證1≤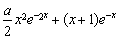 成立,這樣只需利用導數求
成立,這樣只需利用導數求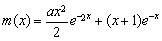 的最小值即可.
的最小值即可.
(Ⅲ)要使f(x0)>x0+1成立,即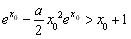 .如果變為
.如果變為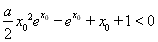 ,那么求導后式子很復雜,故嘗試作其它的變形.
,那么求導后式子很復雜,故嘗試作其它的變形.
變形為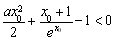 ,要找一個x0>0使該不等式成立,只需找到函數
,要找一個x0>0使該不等式成立,只需找到函數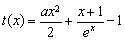 的最小值,滿足
的最小值,滿足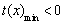 即可.這利用導數就容易解決了.
即可.這利用導數就容易解決了.
試題解析:(I)∵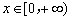 時,
時,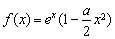 ,
,
∴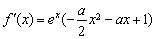 .
.
由題意,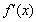 ≥0在
≥0在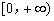 上恒成立,
上恒成立,
當a=0時,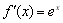 >0恒成立,即滿足條件.
>0恒成立,即滿足條件.
當a≠0時,要使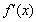 ≥0,而ex>0恒成立,
≥0,而ex>0恒成立,
故只需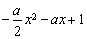 ≥0在
≥0在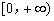 上恒成立,即
上恒成立,即
 解得a<0.
解得a<0.
綜上,a的取值范圍為a≤0. 4分
(Ⅱ)由題知f(x)≤x+1即為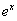 -
-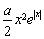 ≤x+1.
≤x+1.
①在x≥0時,要證明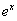 -
-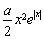 ≤x+1成立,
≤x+1成立,
只需證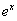 ≤
≤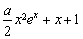 ,即證1≤
,即證1≤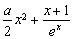 , ①
, ①
令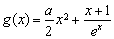 ,得
,得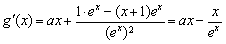 ,
,
整理得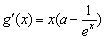 ,
,
∵x≥0時,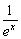 ≤1,結合a≥1,得
≤1,結合a≥1,得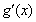 ≥0,
≥0,
∴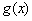 為在
為在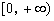 上是增函數,故g(x)≥g(0)=1,從而①式得證.
上是增函數,故g(x)≥g(0)=1,從而①式得證.
②在x≤0時,要使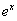 -
-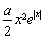 ≤x+1成立,
≤x+1成立,
只需證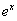 ≤
≤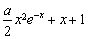 ,即證1≤
,即證1≤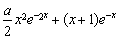 , ②
, ②
令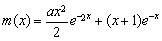 ,得
,得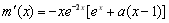 ,
,
而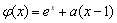 在x≤0時為增函數,
在x≤0時為增函數,
故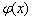 ≤
≤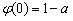 ≤0,從而
≤0,從而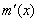 ≤0,
≤0,
∴m(x)在x≤0時為減函數,則m(x)≥m(0)=1,從而②式得證.
綜上所述,原不等式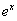 -
-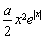 ≤x+1即f(x)≤x+1在a≥1時恒成立. 10分
≤x+1即f(x)≤x+1在a≥1時恒成立. 10分
(Ⅲ)要使f(x0)>x0+1成立,即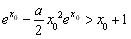 ,
,
變形為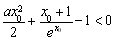 , ③
, ③
要找一個x0>0使③式成立,只需找到函數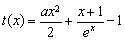 的最小值,滿足
的最小值,滿足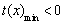 即可.
即可.
∵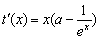 ,
,
令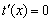 得
得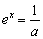 ,則x=-lna,取x0=-lna,
,則x=-lna,取x0=-lna,
在0<x<-lna時,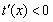 ,在x>-lna時,
,在x>-lna時,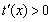 ,
,
即t(x)在(0,-lna)上是減函數,在(-lna,+∞)上是增函數,
∴當x=-lna時,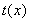 取得最小值
取得最小值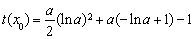
下面只需證明: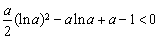 在
在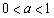 時成立即可.
時成立即可.
又令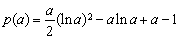 ,
,
則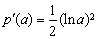 ≥0,從而
≥0,從而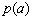 在(0,1)上是增函數,
在(0,1)上是增函數,
則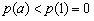 ,從而
,從而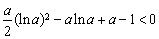 ,得證.
,得證.
于是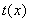 的最小值
的最小值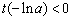 ,
,
因此可找到一個常數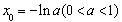 ,使得③式成立. 14分
,使得③式成立. 14分
考點:導數與不等式


科目:高中數學 來源:2013-2014學年上海市長寧區高三上學期教學質量檢測理科數學試卷(解析版) 題型:解答題
已知函數 ,
,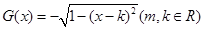
(1)若 是常數,問當
是常數,問當 滿足什么條件時,函數
滿足什么條件時,函數 有最大值,并求出
有最大值,并求出 取最大值時
取最大值時 的值;
的值;
(2)是否存在實數對 同時滿足條件:(甲)
同時滿足條件:(甲) 取最大值時
取最大值時 的值與
的值與 取最小值的
取最小值的 值相同,(乙)
值相同,(乙) ?
?
(3)把滿足條件(甲)的實數對 的集合記作A,設
的集合記作A,設 ,求使
,求使 的
的 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源:2012屆山西大學附中高三4月月考理科數學試卷(解析版) 題型:解答題
(本小題滿分12分)已知函數 ,其中
,其中 .
.
(Ⅰ)若 是
是 的極值點,求
的極值點,求 的值;
的值;
(Ⅱ)求 的單調區間;
的單調區間;
(Ⅲ)若 在
在 上的最大值是
上的最大值是 ,求
,求 的取值范圍 .
的取值范圍 .
查看答案和解析>>
科目:高中數學 來源:2013屆安徽省蚌埠市高二下學期期中聯考理科數學試卷(解析版) 題型:解答題
(本題滿分12分)
已知函數 ,
,
(1)若 是
是 的極值點,求
的極值點,求 值;
值;
(2)若函數 在
在 上是增函數,求實數
上是增函數,求實數 的取值范圍;
的取值范圍;
查看答案和解析>>
科目:高中數學 來源:2011-2012學年甘肅省高三第二次診斷性考試理科數學試卷 題型:解答題
(本小題滿分14分)已知函數 ,其中
,其中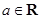 .
.
(Ⅰ)若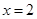 是
是 的極值點,求
的極值點,求 的值;
的值;
(Ⅱ)求 的單調區間;
的單調區間;
(Ⅲ)若 在
在 上的最大值是
上的最大值是 ,求
,求 的取值范圍)
的取值范圍)
查看答案和解析>>
科目:高中數學 來源:2011-2012學年四川省高三2月月考理科數學 題型:解答題
已知函數 ,其中
,其中 .
.
(Ⅰ)若 是
是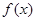 的極值點,求
的極值點,求 的值;
的值;
(Ⅱ)求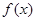 的單調區間;
的單調區間;
(Ⅲ)若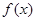 在
在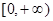 上的最大值是
上的最大值是 ,求
,求 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com