
已知 ,
, ,
, .
.
(1)當 時,試比較
時,試比較 與
與 的大小關系;
的大小關系;
(2)猜想 與
與 的大小關系,并給出證明.
的大小關系,并給出證明.
(1)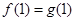 ,
, ,
,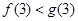 ;(2)猜想:對一切
;(2)猜想:對一切 ,
,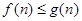 ,證明詳見解析.
,證明詳見解析.
解析試題分析:(1)由 的公式分別計算出
的公式分別計算出 時的
時的 及
及 的值,進而可得比較它們的大小關系;(2)用數學歸納法證明,由(1)可知,
的值,進而可得比較它們的大小關系;(2)用數學歸納法證明,由(1)可知,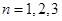 時,不等式顯然成立,接著假設
時,不等式顯然成立,接著假設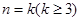 時不等式成立,進而只須證明
時不等式成立,進而只須證明 時不等式也成立即可,在證明
時不等式也成立即可,在證明 時,又只須將
時,又只須將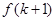 變形為
變形為 ,之后只須用比較法比較判斷
,之后只須用比較法比較判斷 與
與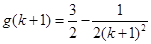 大小,即可證明本題.
大小,即可證明本題.
(1) 當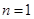 時,
時,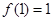 ,
,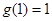 ,所以
,所以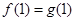 1分
1分
當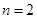 時,
時,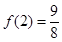 ,
,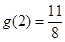 ,所以
,所以 2分
2分
當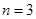 時,
時,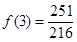 ,
,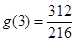 ,所以
,所以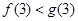 4分
4分
(2) 由(1),猜想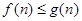 ,下面用數學歸納法給出證明 6分
,下面用數學歸納法給出證明 6分
①當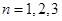 時,不等式顯然成立 7分
時,不等式顯然成立 7分
②假設當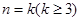 時不等式成立,即
時不等式成立,即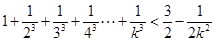 9分
9分
那么,當 時,
時,  11分
11分
因為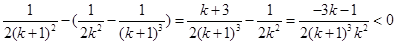 14分
14分
所以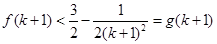 15分
15分
由①、②可知,對一切 ,都有
,都有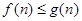 成立 16分.
成立 16分.
考點:數學歸納法.


 云南師大附小一線名師提優作業系列答案
云南師大附小一線名師提優作業系列答案 沖刺100分單元優化練考卷系列答案
沖刺100分單元優化練考卷系列答案科目:高中數學 來源: 題型:解答題
設數列{an}:1,-2,-2,3,3,3,-4,-4,-4,-4,…,(-1)k-1k,…,(-1) ,即當
,即當 (k∈N*)時,an=(-1)k-1k,記Sn=a1+a2+…+an(n∈N*),用數學歸納法證明Si(2i+1)=-i(2i+1)(i∈N*).
(k∈N*)時,an=(-1)k-1k,記Sn=a1+a2+…+an(n∈N*),用數學歸納法證明Si(2i+1)=-i(2i+1)(i∈N*).
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某同學在一次研究性學習中發現以下四個不等式都是正確的: ;
; ;
; ;
; .
.
請你觀察這四個不等式:
(1)猜想出一個一般性的結論(用字母表示);
(2)證明你的結論.
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
在平面幾何里,有:“若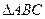 的三邊長分別為
的三邊長分別為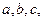 內切圓半徑為
內切圓半徑為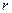 ,則三角形面積為
,則三角形面積為 ”,拓展到空間,類比上述結論,“若四面體
”,拓展到空間,類比上述結論,“若四面體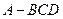 的四個面的面積分別為
的四個面的面積分別為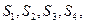 內切球的半徑為
內切球的半徑為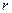 ,則四面體的體積為 ”
,則四面體的體積為 ”
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com